To briefly summarize I&J, they formulate the FTA in bayesian terms. We already know that life exists, as part of our background knowledge. The new piece of evidence put forth by the FTA is that the universe is such that life may arise naturalistically (ie it is "life-friendly"). I&J say the problem is that this evidence argues against supernaturalism, not in favor of it. After all, in a naturalistic world, we must observe that the universe is life-friendly. In a supernaturalistic world, we might observe otherwise, since supernatural intervention can create or sustain life even when natural laws are not life-friendly.
In formal terms:2
N = universe is naturalisticI think their theorem is basically incontrovertible,3 and I do not contest it. However, I feel it is missing the point. Here I aim to explain why.
L = life exists
F = universe is life-friendly
I&J show that
P(N|F&L) ≥ P(N|L)
Whereas the FTA requires that
P(N|F&L) << P(N|L)
What does the Fine-Tuning argument argue?
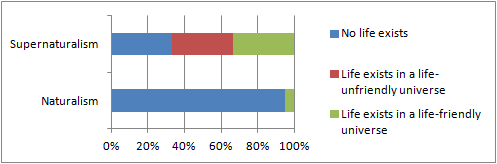
A schematic illustration of the Fine-Tuning argument. The two rows each represent a different meta-theory of the universe. The colored bars represent the probabilities of different events within those meta-theories.
The FTA asks us to compare two meta-theories of the universe: naturalism and supernaturalism. In a naturalistic universe, there's a very small probability that life can arise, because the universal constants need to be just right (or so the argument goes). In a supernatural universe, well, who knows?
I&J make two important points about this argument. First, they argue that the premise is irrelevant, and the conclusion is a fallacy. Formally:
Premise: P(F|N) << 1I checked to see if this is in fact the premise and conclusion used by FTA proponents. The Discovery Institute basically makes the following argument:
Fallacious conclusion: P(N|F) << 1
Premise: P(F|N) < P(F|~N)This is similar to the fallacious reasoning identified by I&J, only it's not fallacious. It's correct. But it requires a stronger premise. Namely, we have to assume that the probability of life under naturalism is less than the probability of life under supernaturalism (as illustrated above).
Conclusion: P(N|F) < P(N)
I believe that I&J reject this stronger premise, and I think this is reasonable. Who is to say that a deity would be particularly likely to arrange the universe such that it contains life? There are an infinite number of possible deities which each prefer a different configuration of the universe. If we only speak of deities that have an inclination towards universes with life, then they're likely to create life, but this is just some sort of selection bias on our part.
But even though I tentatively agree with I&J's first point, I will ignore it for the rest of the post, because I wish to evaluate how their second point stands on its own.
I&J's second point is that we need to include all evidence in our Bayesian. We know two things: life exists, and life can arise. The probability of naturalism should be conditioned on both these facts, not just one or the other. Formally:
FTA argues that P(N|F) > P(N)
But the relevant comparison is between the quantitities P(N|F&L) and P(N|L)
On the other hand, if we compare the size of the green bars, it seems like the FTA works. If the universe is life-friendly, that is evidence for naturalism. But if the universe has life in it, it seems like that's even stronger evidence for the supernatural. In formal terms, it appears that
P(N|F&L) ≥ P(N|L) << P(N)And that's why I feel I&J have missed the point.
Life-friendliness vs Life
The "fine tuning" argument isn't "What do you think about God, when you learn that you are alive?" but "What do you think about God, when you learn that the universe is (apparently) fine-tuned or life-friendly?"As in the quote above, I&J believe that the only piece of evidence advanced by the FTA is that the universe is life-friendly. The existence of life is not a piece of evidence, because we already knew life existed.
--Ikeda & Jefferys
The thing is, the distinction between "life exists" and "life can arise naturalistically" is a novel idea by I&J. It is definitely a useful distinction that improves our understanding of the problem. But I don't think FTA proponents ever make this distinction. FTA proponents are vague about it, and may not even know themselves whether they are arguing about life-friendliness or life-existence.
Therefore, when I&J say that FTA proponents are using life-friendliness as evidence, and not life-existence, this is totally groundless.
To understand the distinction between life-friendliness and the existence of life, it may help to consider how we might demonstrate life-friendliness. It's actually very difficult to demonstrate without any sort of presumption of naturalism. I&J indirectly mention the triple-alpha process, wherein the helium inside of stars fuse to carbon. Since the triple-alpha process is necessary to naturalistically produce carbon life-forms, Fred Hoyle predicted in the 1950s that there was a particular resonance which greatly increased the probability of the triple-alpha process. This prediction was later confirmed.
If FTA proponents are truly using life-friendliness as their evidence, they would point to Fred Hoyle's confirmed prediction. In Biologos treatment, they do discuss the triple-alpha process, but do not mention Hoyle's confirmed prediction. Instead they talk about how "statistically unusual" the resonance is.
Put in formal terms, I&J say that we should compare the quantities P(N|F&L) and P(N|L), because this is the correct comparison, and because this is the comparison described by FTA proponents themselves. But I think that FTA proponents are actually comparing P(N|F&L) and P(N). Furthermore, I think FTA proponents have chosen the correct comparison, whereas I&J have chosen the wrong one.
Trickiness with priors
But what is P(N|L)/P(~N|L)? Why, it is just the prior odds ratio that You assign to describe Your relative belief in N and ~N before You learn that F is true.According to I&J, our prior beliefs are based on our knowledge that life exists. We think, therefore we are. Therefore, if upon seeing that life exists, you think that supernaturalism is more likely than naturalism, then you have a "prior commitment" to supernaturalism.
--Ikeda & Jefferys
"Prior commitment" sounds bad, like you've decided your conclusions before you've considered the evidence. But generally speaking, there's nothing wrong with coming to conclusions without evidence, if you have an a priori argument. Since FTA proponents are arguing about the quantity P(N|L), which I&J call a prior probability, we could say that FTA is partly an a priori argument.
Is it really true that the FTA is an a priori argument? If the only evidence advanced is the existence of life, then the FTA is quite similar to the cosmological argument. The cosmological argument only advances the evidence that there exists something rather than nothing. Is the cosmological argument considered an a priori argument? The internet consensus seems to be not.4
If the FTA is not an a priori argument, then I&J have made an error in using P(N|L) as our prior belief, rather than P(N). If the FTA is an a priori argument, then I&J have basically ignored the a priori component of it, and no wonder that what remains is so unconvincing.
Of course, it seems like FTA proponents really are trying to advance some sort of evidence, and that's why they talk about universal constants and the triple-alpha process. I propose that what's happening is that we're actually comparing three meta-theories:
By eliminating the naturalistic theories where fine-tuning is not necessary, it seems we greatly reduce the probability of life existing within naturalism.
Conclusion (TL;DR)
Ikeda and Jefferys refute the Fine-Tuning argument by making an interesting and useful distinction between universes with life, and universes where life can arise naturally. According to them, it is only necessary to consider the evidence that life can arise naturally. The problem is that this ignores the main thrust of the Fine-Tuning argument.
To refute the Fine-Tuning argument, we must discuss its many other problems, and not the particular problem put forth by Ikeda and Jefferys.
--------------------------------------------
1. Also see the same paper hosted on a different website with inferior design, but with the extra Appendix 2.
2. If you are unfamiliar with the formalism of conditional probabilities, you can read up on it. In this post, I will try to minimize formalism, but it is impossible to eliminate it entirely.
3. The only assumption is that P(~F&L&N) = 0, which is true from the definition of F.
4. See here, here, and here, all search results for the cosmological argument.











12 comments:
I'm unconvinced by your argument.
First, I think you have misidentified the DI's argument. The conclusion that P(N|F) < P(N) doesn't seem to say anything meaningful. I haven't actually parsed their argument, but the conclusion would seem to have to be P(N|F) < P(~N|F).
Therefore, when I&J say that FTA proponents are using life-friendliness as evidence, and not life-existence, this is totally groundless.
I think you are unnecessarily splitting hairs here. I think a more charitable interpretation of I&J's point would be: "If we charitable interpret the FTA argument (which has many flaws) in one particularly way, which removes some of the violence they do to standard probability theory*, then their argument must be invalid.
Similarly,
To refute the Fine-Tuning argument, we must discuss its many other problems, and not the particular problem put forth by Ikeda and Jefferys.
To refute the FTA, we must discuss all its particular problems; I&J discuss one of those particular problems. When an argument is so massively fallacious on so many levels as the FTA, no single argument can possibly refute all of them.
*Anyone is, of course, free to proffer an alternative theory of probability, but then they would have to justify the model and its interpretation independently.
Is the cosmological argument considered an a priori argument? The internet consensus seems to be not.
I dunno. Regardless of what the internet might think, I don't see how the cosmological argument can be interpreted as anything but an a priori argument.
But what is P(N|L)/P(~N|L)? Why, it is just the prior odds ratio that You assign to describe Your relative belief in N and ~N before You learn that F is true.
That is one meaningful interpretation of a Bayesian prior. But we have to be very careful here. If we arbitrarily (and legitimately) assign prior beliefs, then Bayesian theory no longer tells us anything at all about the probability that something is actually true; it tells us only the quality of evidence necessary to change the prior belief.
If we want Bayes to tell us the probability that something is actually true, then we have to independently justify the priors.
There are three major forms of the FTA. Conditioned on some evidence, the FTA purports to show one of three things:
1) Strong FTA: It is more probable that the universe has a supernatural origin than a natural origin.
2) Weak FTA: The evidence increases the probability that the universe is supernatural, and decreases the probability that it is natural.
3) Strength of belief FTA: The evidence tells us the maximum strength of the prior commitment necessary to reject the prior.
All three forms fail in characteristic ways. I&J directly refute (1), and indirectly refute (2). Since by definition probabilism is uncertain, no argument can decisively refute (3), but we can show that the prior commitment has to be extremely high.
I would be interested to hear what you consider the most charitable way to interpret the FTA, and how you refute it.
3) Strength of belief FTA: The evidence tells us the maximum strength of the prior commitment necessary to reject the prior that the universe has a supernatural origin.
The relevant section of DI's article is "The Principle Explained". I parse "an observation counts as evidence in favor of the hypothesis" as P(H|O) > P(H). I believe this is the standard way to interpret "evidence" in Bayesian theory, as it remains true for any choice of priors (as long as they are non-zero). Certainly, mere evidence doesn't demonstrate that a hypothesis is most likely to be true (ie it doesn't show P(H|O) > 0.5). It is impossible to demonstrate such a thing without a choice of priors.
I agree that I&J are simply trying to be charitable to the FTA. However, their interpretation is de facto uncharitable, because it removes the main thrust of the argument.
Regardless of what the internet might think, I don't see how the cosmological argument can be interpreted as anything but an a priori argument.
That's one interpretation. My point is that it doesn't matter whether you parse the FTA as an a priori argument or not. If it isn't one, then the relevant prior is P(N), not P(N|L).
If it is one, then I&J ignored the a priori part. They imply that the prior P(N|L) ~ P(~N|L) for an impartial judge, when in fact that is the very issue in question.
There are three major forms of the FTA. Conditioned on some evidence, the FTA purports to show one of three things:
If you are asking which form of FTA I am using, it is (2). I&J more than indirectly refute (2), they reverse it (ie the evidence actually decreases the probability of supernaturalism). I wish to emphasize the strength of their claim. While I believe the FTA fails, it does not fail quite so badly that we can use FTA as an argument for naturalism.
Well... I'm not tremendously interested in whether or not I&J have addressed the correct argument.
I'm more interested letting you know that I don't really understand your own argument. Although I think I have a fair grasp of probability theory, my math is definitely nowhere nearly as good as yours.
Specifically, I don't understand this passage:
With this modification, I&J find that if the universe is life-friendly, this is evidence against the supernatural. This is easy to see in the above figure. If we rule out a life-unfriendly universe (the red bar), this decreases the likelihood of supernaturalism.
On the other hand, if we compare the size of the green bars, it seems like the FTA works. If the universe is life-friendly, that is evidence for naturalism. But if the universe has life in it, it seems like that's even stronger evidence for the supernatural.
The problem is that we can pick only from the green bars; we cannot in principle observe a universe with no life in it. Therefore, observing life cannot change the prior probability.
Suppose, for example, that you have two bins of socks. Bin A contains 9,900 socks and 10,000 gloves, and Bin B contains 100 socks and 19,900 gloves. I know how many socks and gloves are in each bin size of the bins. Without me looking, you randomly choose a sock (with each individual sock having an equal probability), hand it to me, and ask me what is the probability that it came out of bin B. I know that you will only hand me a sock; you will not hand me a glove.
My prior probability that if I look at a random sock, it came out of bin B is 1/100; the fact that you actually handed me a sock doesn't change my prior probability.
Suppose, in contrast, that Bin A contains 9,000 green socks and 500 red socks. Bin A contains 100 black socks. If you hand me a black sock, the probability that it came out of bin B increases above my prior. The prior probability that any sock came out of bin B is 100/10,000; the observation that it's a black sock means that the probability that it came out of bin B is 100/(100+9,000) or 1/91.
Note that this argument is valid regardless of the relative number of socks in each drawer; as long as bin A contains at least one red sock, and bin B contains only black socks, the probability that a black sock came from bin B is higher than the probability that a red or black sock came from bin B.
Without using life-friendliness, we would have to be able to observe a universe without life in it to be able to change our prior probability.
Substitute "green" for "black" above. Sorry. I want to match the color of the bars.
Yes, that sock analogy is good enough to contain the major points of my OP. Let's say bin A has 9,000 green socks, and 1,000 red socks, and 10,000 gloves. Bin B has 100 green socks and 19,900 gloves. I pick a random sock and show you a green sock.
The FTA says, "Look at this green sock, it probably comes from bin A".
I&J say, "We must separate out the observation that it is green from our prior knowledge that it would be a sock. The FTA uses the evidence that the sock is green to argue that it comes from bin A, but in fact this is evidence for bin B."
And my response is, "That's correct, but it ignores the observation that it is a sock. Just because we *knew* we would get a sock does not change the fact that most socks come from bin A and not B."
In some sense, the FTA is a priori in the sense that we already knew we would get a sock. Of course, we need to demonstrate a posteriori that there were very few socks in bin B in the first place.
And how do we have any idea how many green socks there are in bin A? (That is, how do we know that supernatural beings are particularly likely to make life-friendly universes with life in them?) This is the subject of I&J's first point, and it's one I agree with.
And my response is, "That's correct, but it ignores the observation that it is a sock. Just because we *knew* we would get a sock does not change the fact that most socks come from bin A and not B."
Indeed. The fact that we know that it's actually a sock (know that this universe has life) does not change our evaluation of the prior probability, whatever they might happen to be. Therefore, the fact is not evidentiary.
So basically the FTA uses theoretical physics to argue that there are fewer socks in bin B than we previously thought. Do you agree that this argues that our particular sock is less likely to have come from bin B than we previously thought? I don't care if you call it an evidentiary argument or not, it's still an argument to me.
So basically the FTA uses theoretical physics to argue that there are fewer socks in bin B than we previously thought. Do you agree that this argues that our particular sock is less likely to have come from bin B than we previously thought?
I don't think it does. There are several philosophical reasons, and a few statistical reasons.
First, I'm extremely skeptical about the value of statistics applied to a single observation. I haven't delved too deeply into the subject, but the consensus is that a single observation is probably closer to the mean/median than a tail. Since we have seen one universe, and it has life, the conclusion is that the "typical" universe — if that term even has any kind of meaning — has life.
Second, there are too many dimensions and variables even considering a natural universe to make any confident assertions about the distribution of universes (again, assuming that it makes any kind of sense to talk about distributions of universes). Talking about distributions is even more problematic when we talk about supernaturalism. I think one could make the case that the set of supernatural universes that contain life (much less are life-friendly) is necessarily of measure zero; making any finite natural universe with life infinitely more likely.
Statistically, the FTA says that if you believe life is evidence of supernaturalism, then life is evidence of supernaturalism. That's not an argument except in the sense that a trivially fallacious argument is indeed an argument.
Stated another way, statistically, P(N) and P(~N) are undefined; the P function assumes all events can be observed with equal probability. But we cannot observe any universe without life. Thus, the relevant P functions are P(L)=1 and P(N&L) = 1 - P(~N&L). Assuming your premise is again nothing but the most trivially bad kind of argument.
If you think these are arguments worthy of investigation, knock yourself out. My only disagreement is that I think I&J have picked out the an extremely "interesting" perhaps the only interesting version, of the FTA.
I think all the other formulations have legs only because statistics are really hard, and lay people are easily fooled by statistical arguments that someone with even a modicum of expertise would quickly reject.
But "interesting" is subjective. If you think the relative size argument is interesting, I won't complain. There are many ways to combat ignorance, and I'm not going to say you have to do it my way.
The sock problem seems pretty well-defined to me. Pick a random sock from a set. If we find that most of that set is within bin A, then bin A is the most likely source of the sock.
I think most of your objections are not based on the sock problem, but rather the disanalogies between the sock problem and the FTA. And that is fine and good. The universe is not repeatable like the sock experiment is. The probability measure isn't well-defined like with the socks. Nobody knows how many socks there are in the supernaturalism bin.
I agree with most of these objections to the FTA. I don't agree with objections that apply both to the FTA and to the sock problem. I&J's objection is in this latter category.
Perhaps more importantly, I don't agree with objections that apply both to the FTA and to the weighing of different cosmological theories. If you have cosmological theories A and B, then P(A) and P(B) aren't really well defined. But given observation O (which could be the observation that life exists, or anything else), P(O|A) and P(O|B) are well-defined, if difficult to calculate. The point is to gather enough evidence that P(A|O) >> P(B|O) for a wide range of priors. The fact that there is only one universe we can observe doesn't seem like much of a problem to me.
In the past I've noted that the FTA is a better argument for a multiverse theory than it is for a supernatural theory. I tend to reject the FTA argument for multiverses, so of course I should reject the FTA argument for supernaturalism as well.
There's a major "stuff we don't know about" factor. If we even have a 10% belief that the universal constants are predetermined rather than random, or that something else is going on, then this greatly undercuts the argument.
Post a Comment