When you rotate a three dimensional object, it always rotates around an imaginary line that we call the "axis of rotation". If the object we rotate is a wheel, then the axis of rotation goes through the axel. If you roll a spherical ball on the ground, the axis of rotation is perpendicular to the ball's path, and goes through the ball's center.
Well, if we want to know how "hard" it is to stop the object, then we need to find a certain value called "angular momentum". The angular momentum of any bit of matter is equal to its distance from the axis of rotation, times the mass, times how quickly it goes around the axis of rotation. Of course, your typical object is not a "bit" of matter, but an infinite number of bits of matter. To find the total angular momentum, we just sum up the angular momentum of all the little bits.
The problem with this simplistic view is that it ignores that objects can spin in many directions. To specify the direction of rotation, we say that the angular momentum goes in the same direction as the axis of rotation. If you look in the direction of angular momentum, the object will always appear to be rotating clockwise. If you rotate a standard screw, it moves in the direction of angular momentum.
Now, precession explained!
What is precession? Precession is when the axis of rotation itself spins. For example, when a gyroscope wobbles, its axis of rotation is first tilted north, then east, then south, and west. Its axis of rotation continues to change directions, moving around in a circle. It is important to remember that the axis of rotation is not in itself a physical object, so we would not expect it to spin unless there was some cool physics afoot. There is.
Angular momentum is just like regular motion: it does not change unless something pushes the object. In physics terms, we apply a force to the object. But force alone does not change angular momentum. For example, let's say we have a balance scale.
If we push straight down on the yellow circle, the two arms are not going to start rotating. However, if we push down on one of the arms, it will start moving. The further from the center we push, the less force it takes to move the scale.The rate at which the angular momentum changes is equal to a value called "torque". Torque is equal to the amount of force times the distance from the axis of rotation. The reason it is easier to push the scale when further from the center is that it takes a smaller amount of force to create the same amount of torque. Torque, just like angular momentum, has a direction. If you apply torque, it will cause an object to change its angular momentum in the same direction as the torque you applied.
Now that we know about torque, let's look at a simple wheel with an axel. One end of the axel is hanging from a string. Excuse my poor art.
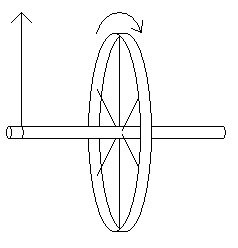In case it isn't clear, the wheel is rotating in the direction of the arrow in the middle, and the string is applying a force in the direction of the arrow on the left. The angular momentum of this wheel goes to the right.Which way does the torque go? Well, if the wheel weren't spinning, then it would simply fall so that the axel is vertical. This fall would cause the wheel to spin clockwise from our point of view. Therefore, the torque is going into the page (forward, in the direction we are looking). This causes the angular momentum to move into the page.
However, once the angular momentum starts going into the page, the entire wheel turns. The direction of the torque has also turned, and is now facing left. The more the wheel turns, the more the direction of the torque turns. As a result, the angular momentum will perpetually go around in circles, chasing after the torque. And that's what causes precession.
Now, all of this is difficult to understand, except by resorting to math (yes, we were doing math, albeit simplified math). I can conceptually visualize special relativity, and the fourth dimension, but precession? That's hard. I believe that is the sentiment behind this comic strip from xkcd.
Next time: Precession as applied to Earth!
10 comments:
You say, "If you look in the direction of angular momentum, the object will always appear to be rotating clockwise." This does not make sense to me. When you look in the direction of the angular momentum, it is the same as looking at the edge of the clock, and the word "clockwise" has no meaning. The words "clockwise" and "counterclockwise" only have meaning when one views the object along the axis of rotation. Can you clarify this?
When you look in the direction of angular momentum, you are not looking at the edge of the clock, but at the face of the clock. By definition, the angular momentum is parallel to the the axis of rotation. We use this definition precisely because it is the only direction in which "clockwise" and "counter-clockwise" can have meaning.
Feel free to ask for more clarifications. I realize my writing is not always particularly clear. It is a central problem of communication--everything is so much more articulate in my head!
"Well, if the wheel weren't spinning, then it would simply fall so that the axel is vertical. This fall would cause the wheel to spin clockwise from our point of view. Therefore, the torque is going into the page (forward, in the direction we are looking). This causes the angular momentum to move into the page." I am not sure I understand what you mean. Torque applied to one side of the wheel going into the page is the same as torque applied to the other side coming out of the page, is it not? Can you clarify this further?
Torque is defined as the cross-product of the radius vector and the force vector. A cross-product of two vectors results in a third vector that is perpendicular to the other two.
The force vector is going in the direction of the string--up. The radius vector goes from the center of mass to the location of the string--to the left. The torque must therefore go in a direction that is perpendicular to both the "up" and "left" directions. Therefore, the torque either goes forwards or backwards (we have to think in 3d here: "into the page" just means "forward").
To determine whether it goes forwards or backwards, we use the "right-hand rule". That basically means that torque in the forward direction causes clockwise rotation as opposed to counter-clockwise.
We could also use a "left-hand rule", but you have to stick to one rule or the other, and the right-hand rule is the one that we chose.
Since the force from the string would cause the wheel to rotate clockwise, the torque must be going forwards as opposed to backwards. This is what I was trying to explain in the original post.
Summary: Force goes up. Radius vector goes left. Torque goes forward. Angular momentum goes right, but is changing in the direction of torque.
In this particular situation, we are not applying torque to one side of the object or the other. Torque is applied to the object as a whole. However, the force is being applied to one side of the wheel.
A string on the left would cause torque going into the page and a string on the right would cause torque coming out of the page. Was that what you were thinking?
I still don’t get it. When you hang onto one end of the axel with a string, and drop the other end with the wheel, you are applying a downward force (gravity) to the wheel at its center of mass, which is the point at which the axel passes through the wheel. Since this force is applied at the center of rotation of the rotatable object (the wheel) and not at some distance from the center of rotation, no torque is applied to the wheel. Now, if you consider the entire object (the wheel plus the axel), you are applying a force (gravity) to the center of mass of the entire object, and the center of rotation is now the point at which the axel hangs from the string, so you are applying torque to the entire object. (Incidentally, I’m consulting Halliday, Resnick, and Walker, “Fundamentals of Physics,” 4th edition, pp. 300-301.)
Yes, there are actually two forces, one from the string and one from gravity. If we omit either of the forces, the wheel either falls to the ground, or falls into the sky.
The "center of rotation" is actually an arbitrarily chosen point, but we usually choose the center of mass for simplicity's sake. You can also define it to be the point where the string is attached to the axel. This is equivalent to saying that the wheel is spinning around its center of mass while the center of mass is moving around in a circle. Depending on our choice, we either say that the force of gravity is causing torque, or that the string is causing torque.
Once the object is precessing, you are correct that the entire wheel rotates around the point where the string is attached to the axel. But it is rotating at a constant rate (at least at equilibrium), so no vertical torque is necessary.
Thank you very much, i finally understand the wheel experiment on precession my teacher had demonstrated at school, once i read this page. I LOVE YOU MILLER.
You may or may not ever read this comment as the conversation you had here before happened in 2007, so could anyone who read this and gets it tell me whether or not I'm right.
The angular momentum of the wheel which is spinning around the axel is described by the (pseudo-)vector which is pointing right. I will call this L1.
As both gravity and the rope exert a force on the entire system of both the axel and the wheel, this system will rotate around the point at which the axel is hang to the rope. The angular momentum the entire system gets is described by a (pseudo-)vector L2 which points into the screen. Summary: the combined force of the rope and gravity result in a torque into the screen, which results in a angular momentum into the screen.
So if I get it right, angular momentum L1 is affected by the torque and therefore starts to turn into that direction? But why doesn't L1 just keeps pointing in that direction and the torque results in a angular momentum L2?
Yes, you're almost correct. It's not angular momentum (L2) which is pointing into the screen, but a torque (hereby called T2) which is pointing into the screen.
Torque is nothing more than the time-derivative of the angular momentum. So L1 will move in the direction of T2. But when L1 changes direction, the entire axle of the wheel changes with it. And when the axle changes direction, T2 also changes direction.
The end result is that L1, T2, and the axle will all continuously rotate in a circle. L1 and T2 will always be 90 degrees apart, so it never stops (until energy is lost to friction).
IMHO, my physics explanations from 2007 weren't that good, but hopefully by now my explaining skills are improved. You're welcome to ask more questions, and I can guarantee that I see them.
Post a Comment