Nine/Twelve/Sixteen Dots puzzles
Twelve Dots solution
Pause. You still have a chance to solve the Sixteen Dots puzzle.
Sixteen Dots solution
Wednesday, November 28, 2007
Tuesday, November 27, 2007
Observation shortens the universe's life?
A reader showed me a recent article in the Telegraph: Mankind 'shortening the universe's life'. As a resident "physicist" of the blogosphere, I feel obligated to comment. My warning is that the science here is quantum mechanics, and I have not yet received a full formal education about the theory. I may or may not know what I am talking about. For a real physicist's comment, I refer you to Rob Knop, Chad Orzel, or Pamela (Edit: also, John Baez). Another warning is that I usually try to "work my way up" to complicated science like this by explaining the background first, but there will be none of that this time. We're heading into deep waters!
The article is based on a paper in New Scientist. I haven't read the paper, and probably wouldn't understand it, so I can't say whether the Telegraph has over-sensationalized it or if it was New Scientist itself. But the article states that we may be shortening the universe's life expectancy (which is still many billions of years) simply by making astronomical observations of dark energy. Hmm, well... making wild claims might impress the Telegraph, but it just makes me more skeptical.
The first thing I thought was, "Life expectancy?" Last I checked, cosmologists think the universe extends infinitely into the future. The article explains that dark energy, which (allegedly) caused the Big Bang, and currently accelerates the expansion of the universe, may at any point in time cause another Big Bang of sorts. "Any point in time", of course, means that it has a very small chance to occur over any given billion-year period. That sounds pretty iffy to me, where "iffy" means "legitimate, but not well-established". Actually, I suspect this hypothesis is the main topic of the New Scientist paper.
The reason that observing dark matter might affect the age of the universe is because of something called the Quantum Zeno Effect. Perhaps I will fully explain this in the distant future (Cosmic Variance already has), but I'll just summarize for now. The Quantum Zeno Effect is a way of affecting quantum states by making multiple measurements. Each measurement "collapses the wavefunction", which means the quantum state has changed. With enough of these measurements, you can change the quantum state to something completely different from what it would have been otherwise. This is not to be confused with the "observer effect" in which the act of shooting photons at what you want to see changes it. This is a genuine, tested quantum effect that requires no physical contact of any sort. Yes, it is very strange.
I'm not sure of the details, but supposedly observing dark energy may "reset" its quantum state such that the universe's life expectancy shortens. But the problem with this is that it assumes a specific interpretation of quantum mechanics. That is, it assumes that wavefunctions collapse only when humans observe them. See, there are lots of interpretations of quantum mechanics, most of which are mathematically (if not philosophically) equivalent. So if you've got some theory, it should work under all interpretations or none of them. The fact that this theory relies on one specific interpretation makes it suspect in my admittedly uneducated eyes. All the interpretations must come out the same, or you're doing something wrong.
In the unlikely scenario that their idea is correct, I think they are mistaken if they think that quantum state should reset only when scientists try to measure dark energy. I think the wavefunctions collapse as soon as you look into the sky, regardless of whether you decide to do some mathematical calculations afterwards to find how much dark energy there is. For that matter, I think that there is not even any need to look at the sky. If the photons from the sky hit my desk, then merely looking at my desk is an indirect observation of dark energy. Does looking at my desk shorten the lifespan of the universe? I doubt it.
The second half of the article talks about an unrelated story in which a previous measurement of mass turned out to be wrong by a certain amount. I don't know much about that, but it sounds completely legitimate. However, there is a misleading segue between the two stories. This is not a case of measurements changing the universe, just a case of human errors changing measurements.
The article is based on a paper in New Scientist. I haven't read the paper, and probably wouldn't understand it, so I can't say whether the Telegraph has over-sensationalized it or if it was New Scientist itself. But the article states that we may be shortening the universe's life expectancy (which is still many billions of years) simply by making astronomical observations of dark energy. Hmm, well... making wild claims might impress the Telegraph, but it just makes me more skeptical.
The first thing I thought was, "Life expectancy?" Last I checked, cosmologists think the universe extends infinitely into the future. The article explains that dark energy, which (allegedly) caused the Big Bang, and currently accelerates the expansion of the universe, may at any point in time cause another Big Bang of sorts. "Any point in time", of course, means that it has a very small chance to occur over any given billion-year period. That sounds pretty iffy to me, where "iffy" means "legitimate, but not well-established". Actually, I suspect this hypothesis is the main topic of the New Scientist paper.
The reason that observing dark matter might affect the age of the universe is because of something called the Quantum Zeno Effect. Perhaps I will fully explain this in the distant future (Cosmic Variance already has), but I'll just summarize for now. The Quantum Zeno Effect is a way of affecting quantum states by making multiple measurements. Each measurement "collapses the wavefunction", which means the quantum state has changed. With enough of these measurements, you can change the quantum state to something completely different from what it would have been otherwise. This is not to be confused with the "observer effect" in which the act of shooting photons at what you want to see changes it. This is a genuine, tested quantum effect that requires no physical contact of any sort. Yes, it is very strange.
I'm not sure of the details, but supposedly observing dark energy may "reset" its quantum state such that the universe's life expectancy shortens. But the problem with this is that it assumes a specific interpretation of quantum mechanics. That is, it assumes that wavefunctions collapse only when humans observe them. See, there are lots of interpretations of quantum mechanics, most of which are mathematically (if not philosophically) equivalent. So if you've got some theory, it should work under all interpretations or none of them. The fact that this theory relies on one specific interpretation makes it suspect in my admittedly uneducated eyes. All the interpretations must come out the same, or you're doing something wrong.
In the unlikely scenario that their idea is correct, I think they are mistaken if they think that quantum state should reset only when scientists try to measure dark energy. I think the wavefunctions collapse as soon as you look into the sky, regardless of whether you decide to do some mathematical calculations afterwards to find how much dark energy there is. For that matter, I think that there is not even any need to look at the sky. If the photons from the sky hit my desk, then merely looking at my desk is an indirect observation of dark energy. Does looking at my desk shorten the lifespan of the universe? I doubt it.
The second half of the article talks about an unrelated story in which a previous measurement of mass turned out to be wrong by a certain amount. I don't know much about that, but it sounds completely legitimate. However, there is a misleading segue between the two stories. This is not a case of measurements changing the universe, just a case of human errors changing measurements.
Categories:
news,
nonsense,
physics,
quantum mechanics
Sunday, November 25, 2007
CotG #79 and Humanist Symposium
Two carnivals are up today. The Carnival of the Godless is up at the Sexy Secularist, and the Humanist Symposium is up at The Greenbelt. The Carnival of the Godless includes my article Negative ≠ Bad.
It occurs to me that it is not immediately obvious to everyone what exactly a carnival is. A blogging carnival is where someone collects all the best blog postings on a particular topic and puts them together in one big carnival post. In other words, lots of bloggers like me submit their best posts to the carnival host, and the host makes one big post linking to all of the submissions. There are three main carnivals around my subject area: the Skeptic's Circle, about skepticism; the Carnival of the Godless, about godlessness; and the Humanist Symposium, which is specifically about the positive aspects of godlessness. Each occurs every two or three weeks with a different blogger as the host.
Blogging carnivals are a great way to:
It occurs to me that it is not immediately obvious to everyone what exactly a carnival is. A blogging carnival is where someone collects all the best blog postings on a particular topic and puts them together in one big carnival post. In other words, lots of bloggers like me submit their best posts to the carnival host, and the host makes one big post linking to all of the submissions. There are three main carnivals around my subject area: the Skeptic's Circle, about skepticism; the Carnival of the Godless, about godlessness; and the Humanist Symposium, which is specifically about the positive aspects of godlessness. Each occurs every two or three weeks with a different blogger as the host.
Blogging carnivals are a great way to:
- read the best posts on a topic from the past few weeks from all over the blogosphere.
- find new blogs worth reading.
- accumulate readers (from the perspective of a young and ambitious/narcissistic blogger).
Outside of the box
Difficulty: 4 of 10
The Infamous Brick Puzzle seems to be a favorite among googlers. With that thought, I present another classic puzzle that involves drawing lines without lifting your pencil. The Nine Dots puzzle is one of the most well-known puzzles ever. It is the origin of the phrase "Think outside of the box".
 Without lifting your pencil, draw four straight lines such that they go through all nine dots (which, by the way, represent infinitesimally small points). This puzzle is just too famous, so presumably everyone already knows the solution? If not, I will never spoil it for you--I insist that you solve it for yourself! (But of course, I can't stop you from googling "Nine Dots puzzle".)
Without lifting your pencil, draw four straight lines such that they go through all nine dots (which, by the way, represent infinitesimally small points). This puzzle is just too famous, so presumably everyone already knows the solution? If not, I will never spoil it for you--I insist that you solve it for yourself! (But of course, I can't stop you from googling "Nine Dots puzzle".)
So once you've found the solution to the classic, there's still more! I give you two more variations: The Twelve Dots puzzle and the Sixteen Dots puzzle.
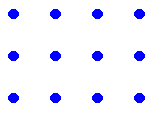 Without lifting your pencil, draw five straight lines through all twelve dots. You must complete a loop, ending where you started. Cross each dot no more than once.
Without lifting your pencil, draw five straight lines through all twelve dots. You must complete a loop, ending where you started. Cross each dot no more than once.
 The Sixteen Dots puzzle is identical to the Twelve Dots puzzle, only you must draw six lines.
The Sixteen Dots puzzle is identical to the Twelve Dots puzzle, only you must draw six lines.
If anyone wants to post a solution in the comments, I suggest listing the coordinates of where you're starting and ending the lines (since it would be difficult to post pictures). Just let the lower left point be the origin or something.
Solutions
The Infamous Brick Puzzle seems to be a favorite among googlers. With that thought, I present another classic puzzle that involves drawing lines without lifting your pencil. The Nine Dots puzzle is one of the most well-known puzzles ever. It is the origin of the phrase "Think outside of the box".
 Without lifting your pencil, draw four straight lines such that they go through all nine dots (which, by the way, represent infinitesimally small points). This puzzle is just too famous, so presumably everyone already knows the solution? If not, I will never spoil it for you--I insist that you solve it for yourself! (But of course, I can't stop you from googling "Nine Dots puzzle".)
Without lifting your pencil, draw four straight lines such that they go through all nine dots (which, by the way, represent infinitesimally small points). This puzzle is just too famous, so presumably everyone already knows the solution? If not, I will never spoil it for you--I insist that you solve it for yourself! (But of course, I can't stop you from googling "Nine Dots puzzle".)So once you've found the solution to the classic, there's still more! I give you two more variations: The Twelve Dots puzzle and the Sixteen Dots puzzle.
 Without lifting your pencil, draw five straight lines through all twelve dots. You must complete a loop, ending where you started. Cross each dot no more than once.
Without lifting your pencil, draw five straight lines through all twelve dots. You must complete a loop, ending where you started. Cross each dot no more than once. The Sixteen Dots puzzle is identical to the Twelve Dots puzzle, only you must draw six lines.
The Sixteen Dots puzzle is identical to the Twelve Dots puzzle, only you must draw six lines.If anyone wants to post a solution in the comments, I suggest listing the coordinates of where you're starting and ending the lines (since it would be difficult to post pictures). Just let the lower left point be the origin or something.
Solutions
Friday, November 23, 2007
Negative ≠ Bad
One of the complaints against atheism, as well as skepticism, is that "it's all so negative!"
Let's break up the complaint into it's two components. First, the complaint states that atheism and skepticism are completely negative. This is not true. Skepticism goes hand in hand with science, which is hardly negative. Atheism often accompanies a ton of positive views (usually including science), though the particular positive views may vary from person to person.
The second component of the complaint is often implicit: "...and negative things are bad."
This is an excellent example of the equivocation fallacy. The equivocation fallacy is when you switch around the meanings of words. For example, let's say I use astronomy to show that stars are gigantic balls of hot gas. I go on to say, "Therefore, Tom Cruise is full of hot air." I've just switched around two meanings of "star"--those things we see in the sky, and those things we see on the screen. I also switched around different meanings of "hot air". In this fictional case with stars, I would probably fool no one with my reasoning, but in practice it is much harder to catch.
The word "Negative" has two meanings. In the first part of the complaint, it means focusing on criticizing claims rather than making new ones. A "negative claim" states what is false rather than what is true. In the second part of the complaint, "negative" means "bad". Just because these two meanings can be signified with the same word doesn't mean we should confuse the two. It's possible that the two meanings are equivalent, but you have to argue that fact.
So why might negative be bad?
Let's break up the complaint into it's two components. First, the complaint states that atheism and skepticism are completely negative. This is not true. Skepticism goes hand in hand with science, which is hardly negative. Atheism often accompanies a ton of positive views (usually including science), though the particular positive views may vary from person to person.
The second component of the complaint is often implicit: "...and negative things are bad."
This is an excellent example of the equivocation fallacy. The equivocation fallacy is when you switch around the meanings of words. For example, let's say I use astronomy to show that stars are gigantic balls of hot gas. I go on to say, "Therefore, Tom Cruise is full of hot air." I've just switched around two meanings of "star"--those things we see in the sky, and those things we see on the screen. I also switched around different meanings of "hot air". In this fictional case with stars, I would probably fool no one with my reasoning, but in practice it is much harder to catch.
The word "Negative" has two meanings. In the first part of the complaint, it means focusing on criticizing claims rather than making new ones. A "negative claim" states what is false rather than what is true. In the second part of the complaint, "negative" means "bad". Just because these two meanings can be signified with the same word doesn't mean we should confuse the two. It's possible that the two meanings are equivalent, but you have to argue that fact.
So why might negative be bad?
- Negative claims practically advertise the things they criticize.
- Negative claims lead to disrespect.
- With what will people replace their previous beliefs?
- Negative claims can't unite anyone.
- There is something to be said about prioritizing claims that have wide acceptance. If we're criticizing a claim that is virtually unknown, then yes, maybe it is a little counterproductive. But religion and pseudoscience are hardly unknown.
- Sure, if a few people have their own self-worth all tied up with their beliefs, maybe it is disrespectful. But such people have already set themselves up for a fall, and deserve a dose of disillusionment. For everyone else, it is actually quite easy to respect the person while disagreeing with them. I do it all the time.
- Positive and negative claims are not mutually exclusive. You can criticize other claims while simultaneously putting forward better ones. But even without our help, it is a mistake to think that people will systematically replace their old beliefs with something worse.
- On the contrary, I think that negative claims often unite many more people. For example, "Atheist" is a largely negative label that only really says what people don't believe. But if you consider more positive labels like "Secular humanist" or "Objectivist", you've just split atheists into a bunch of smaller groups. These groups might be tighter knit, but at the cost of size. So which do you want: a group that loosely unites many people, or a group that tightly unites only a few people? Bad question. We can have both kinds of groups, and both play important roles. So there is no reason to outright reject negativity as a basis for uniting people.
Wednesday, November 21, 2007
Skeptic's Circle #74
Skeptic's Circle #74 is up at Med Journal Watch. It includes my post on the 10% myth. Have fun.
And happy Thanksgiving! For those who don't celebrate, then, umm... happy Thursday!
And happy Thanksgiving! For those who don't celebrate, then, umm... happy Thursday!
"Science makes leap of Faith"
An anonymous reader pointed to me an article in The Daily Breeze called Science makes leap of faith. Time for a bit of fisking, yes?
The article is talking about Nobel winning James Watson's recent racist comments. I seem to recall that the ScienceBlogs were chatting about this (exampes: PZ, Zuska). In brief, James Watson has made it clear that he's a dangerous fool (and misogynist!).
Some quotes from the article:
The article is talking about Nobel winning James Watson's recent racist comments. I seem to recall that the ScienceBlogs were chatting about this (exampes: PZ, Zuska). In brief, James Watson has made it clear that he's a dangerous fool (and misogynist!).
Some quotes from the article:
Why is Watson quelled in pursuing his theory that "There is no firm reason to anticipate that the intellectual capacities of peoples geographically separated in their evolution should prove to have evolved identically"?Yes there is. The timescale is too short. They are not completely isolated. The environments are not significantly different. And if I recall, the usual racial "divisions" often don't match the populations that were actually genetically isolated.
Why all the outrage? All the epithets? All the accusations of racism? All the canceled lectures?Maybe because he's wrong and he's spreading particularly harmful misinformation.
Since I'm not an evolutionist, I need not stick my feet in the muddy waters of this emotionally charged issue - the Bible asserts that all men (regardless of DNA structure) are made in the image of God, and that's enough for me.I get the feeling that "DNA structure" constitutes the totality of this writer's scientific knowledge.
[Naturalists] are generally so quick to point out how Copernicus, Galileo and Darwin took rank against the tide of their day and how we are all better off for it.Galileo Fallacy
Watson is seeking to live this maxim ["No Heaven. No Hell. Just Science."] out to its logical conclusion and what a mess!What?! Is this, like, surrealist performance art? Because all I see are non sequiturs.
All this reveals the vacuum formed with the efforts to oust an ultimate and absolute immaterial being - I think the common term is "God" - from any venue in life.
The scientific community's cannibalization of Watson demonstrates that they have a system of ethics that trumps their academics. But their unwillingness to acknowledge an ultimate and supreme source of ethics naturally results in their divided house where Watson currently sits surrounded by vacancy signs.He is assuming that Watson's comments are academically sound, which they're not. So, garbage in, garbage out, right? But is it just me, or is there more garbage coming out than going in? Let's break this down. He says that there is confusion because scientists are putting ideologies before truth. But it's not the ideology-before-truth thing that's the problem. The problem is that they're going by their own separate ideologies rather than the one supreme ideology (aka Jesus). Oooookay. Someone has not thought this through very clearly.
Monday, November 19, 2007
Replacing the 10% myth
It's often said that we only use 10% of our brains. The other 90% is, of course, filled with penguins. I've got proof, in fictional form!
So in case anyone didn't already know, this is a myth. It's not true that we only use 10% of our brains, nor is it true that only 10% is active at any one point, nor is it true that we understand, or are conscious of only 10%. When I googled the words "10 percent" and "brain" I didn't find a single credulous article until the third page. So I think saying more on this myth is just overkill. Instead, I'll go off on a tangent about how skeptics deal with truth.
Anyways, I think the reason the 10% myth persisted for so long is that people like the point it is meant to make. "Everyone has a lot of hidden potential," is the message. Who are we skeptics to take away from that? It's certainly difficult to think of a case where the 10% myth would actually harm anyone. Well, the myth is occasionally used to justify drug use or belief in "psychics" (aka con artists), but for the moment, let's ignore those possibilities. If it's not hurting anyone, and if people actually find meaning in this myth, why burst their bubbles? Isn't this a slippery slope in which skeptics will start to reject all of life's little lessons and become bitter-hearted cynics?
Not really, no. But I do think we should reject life's little lessons when it turns out they're wrong. If the only way to justify a life lesson is through lies, well then maybe that lesson is wrong. If it requires pseudoscience to inspire people to do something, then maybe people shouldn't be inspired. If people need a myth to find meaning, that meaning might be false. False meaning can still motivate people, but who in the world wants to be motivated by lies?
So is it true that all people have hidden potential? I think so. But it's not because we only use 10% of our brains. Surely, we can think of a good reason without resorting to myths. It is because when we see great men and women, we realize they are not so different from us. That wasn't so hard, was it?
She passed the time quietly in a world of her own in which she was surrounded as far as the eye could see with old cabin trunks full of past memories in which she rummaged with great curiosity, and sometimes bewilderment. Or, at least, about a tenth of the cabin trunks were full of vivid, and often painful or uncomfortable memories of her past life; the other nine-tenths were full of penguins, which surprised her.-Douglas Adams, The Long Dark Teatime of the Soul
So in case anyone didn't already know, this is a myth. It's not true that we only use 10% of our brains, nor is it true that only 10% is active at any one point, nor is it true that we understand, or are conscious of only 10%. When I googled the words "10 percent" and "brain" I didn't find a single credulous article until the third page. So I think saying more on this myth is just overkill. Instead, I'll go off on a tangent about how skeptics deal with truth.
Anyways, I think the reason the 10% myth persisted for so long is that people like the point it is meant to make. "Everyone has a lot of hidden potential," is the message. Who are we skeptics to take away from that? It's certainly difficult to think of a case where the 10% myth would actually harm anyone. Well, the myth is occasionally used to justify drug use or belief in "psychics" (aka con artists), but for the moment, let's ignore those possibilities. If it's not hurting anyone, and if people actually find meaning in this myth, why burst their bubbles? Isn't this a slippery slope in which skeptics will start to reject all of life's little lessons and become bitter-hearted cynics?
Not really, no. But I do think we should reject life's little lessons when it turns out they're wrong. If the only way to justify a life lesson is through lies, well then maybe that lesson is wrong. If it requires pseudoscience to inspire people to do something, then maybe people shouldn't be inspired. If people need a myth to find meaning, that meaning might be false. False meaning can still motivate people, but who in the world wants to be motivated by lies?
So is it true that all people have hidden potential? I think so. But it's not because we only use 10% of our brains. Surely, we can think of a good reason without resorting to myths. It is because when we see great men and women, we realize they are not so different from us. That wasn't so hard, was it?
Sunday, November 18, 2007
I can't keep this up
I've been sustaining a steady update schedule of once per day, but I don't think I'll be able to maintain it forever. I can't be like PZ who keeps an average of 6 or 7 posts a day (no exaggeration!), or the Friendly Atheist, who averages about 3. Part of it is that this is mostly original writing, and I don't get a ton of e-mail asking me to comment on this or that news story. (Again, I will not make public an e-mail address unless there is enough demand for one.)
I am a student with other uses for my time, so I'd like to slow down the schedule. Let's try once every two days. I might also take my Thanksgiving holiday. If you're really bored, I suggest looking at my sidebar links. There's my blogroll (on which only awesome blogs are allowed), the ever-nifty atheist blogroll, and some other stuff.
In other news, I am now googlable. I'm on the first page of a search of "tangent time" (even without quotes). It's so awesome.
I am a student with other uses for my time, so I'd like to slow down the schedule. Let's try once every two days. I might also take my Thanksgiving holiday. If you're really bored, I suggest looking at my sidebar links. There's my blogroll (on which only awesome blogs are allowed), the ever-nifty atheist blogroll, and some other stuff.
In other news, I am now googlable. I'm on the first page of a search of "tangent time" (even without quotes). It's so awesome.
Saturday, November 17, 2007
Moving goalposts
As I said before, I think it's important that we not blindly apply logical fallacies as if they were infallible. Well the "moving goalposts" fallacy is one that I think should not be considered a fallacy at all, though for different reasons from the previous examples. Most skeptics would disagree with me, so I'll argue my point.
The "moving goalposts" fallacy starts out when, in a debate between Alice and Bob*, Alice sets a "goalpost" for Bob. Alice says, "If you can do X, you will have proven me wrong." Bob proceeds to do X. Alice seems to forget what she had previously said, and now says, "If you can do Y, I will eat my words." Bob proceeds to do Y. Alice again seems to forget, and now says, "If you can do Z, I will put my foot in my mouth." Bob becomes frustrated and gives up.
The idea behind this fallacy is that even though Bob has disproven Alice's claim twice, Alice does not recognize that she has lost. If action X does in fact disprove Alice's claim, and if Alice does not change her claim, then, yes, Alice is in the wrong. She is also in the wrong if she merely changes the name of her claim, or otherwise equivocates what she really thinks. She is doing the rhetorical equivalent of sticking her fingers in her ears and singing loudly, "I know I'm right and you're wrong because I haven't heard any evidence!"
But I think that in practice, this is not what usually happens. In practice, Alice changes her position. Her change in position may have been very slight, and implicit, but it is a change nonetheless. Perhaps she has decided that X does not in fact disprove her original claim. Other times, Alice may change her original claim slightly to accommodate the evidence from X. I do not see why changing one's own position should be considered in itself fallacious.
However frustrated Bob may be, he must provide a new argument against Alice's new claim. Either that, or Bob may point out that his previous arguments still apply to Alice's new claim. There are innumerable wrong positions Alice could take. Must Bob counter every single one that Alice decides to take? Yes, at least if Bob wants to convince Alice. Perhaps he can think up an argument that counters all possible positions Alice could take.
I think what people really find frustrating about moving goalposts is that they want their opponent to definitively lose. Bob wants Alice to publicly admit complete defeat. But instead of admitting defeat, Alice merely decides to replace her old claim with a new, slightly different one. But I would say that the desire for a clear surrender is an emotional one. In a way, Alice has admitted defeat by discarding her old position. She just hasn't done it loudly or theatrically. They seem to fantasize about their opponents saying, "I was a fool, and you are wise." Take what you can get, I say. The real goal of debate isn't victory, it's truth.
Rather than just talking about Alice and Bob, allow me to substitute a real life example. Many people think of "Intelligent Design" as being Creationism with a moved goalpost. Well, I think that means you can't always use the same arguments against the two. On the one hand, you could argue against both ID and Creationism by pointing out that Evolution is really one of the best established theories in all of science. On the other hand, you couldn't argue against ID by pointing out evidence of a 4.6 billion year history, because (as far as I know) ID already accepts the age of Earth. ID has a ton of problems, but it's still a slight step above Creationism. I just don't see the goalpost-moving as being in itself fallacious. Are people not allowed to change their minds, to improve their own positions?
Well, I guess in this case it's reasonable to want a definitive loss, but that's only because ID isn't so much a real debate as it is a silly PR machine.
*In case it isn't clear, Alice and Bob are just two names I am using to represent any two people in a debate. Physicists seem to be fond of using these two particular names in thought experiments, so I will do the same.
The "moving goalposts" fallacy starts out when, in a debate between Alice and Bob*, Alice sets a "goalpost" for Bob. Alice says, "If you can do X, you will have proven me wrong." Bob proceeds to do X. Alice seems to forget what she had previously said, and now says, "If you can do Y, I will eat my words." Bob proceeds to do Y. Alice again seems to forget, and now says, "If you can do Z, I will put my foot in my mouth." Bob becomes frustrated and gives up.
The idea behind this fallacy is that even though Bob has disproven Alice's claim twice, Alice does not recognize that she has lost. If action X does in fact disprove Alice's claim, and if Alice does not change her claim, then, yes, Alice is in the wrong. She is also in the wrong if she merely changes the name of her claim, or otherwise equivocates what she really thinks. She is doing the rhetorical equivalent of sticking her fingers in her ears and singing loudly, "I know I'm right and you're wrong because I haven't heard any evidence!"
But I think that in practice, this is not what usually happens. In practice, Alice changes her position. Her change in position may have been very slight, and implicit, but it is a change nonetheless. Perhaps she has decided that X does not in fact disprove her original claim. Other times, Alice may change her original claim slightly to accommodate the evidence from X. I do not see why changing one's own position should be considered in itself fallacious.
However frustrated Bob may be, he must provide a new argument against Alice's new claim. Either that, or Bob may point out that his previous arguments still apply to Alice's new claim. There are innumerable wrong positions Alice could take. Must Bob counter every single one that Alice decides to take? Yes, at least if Bob wants to convince Alice. Perhaps he can think up an argument that counters all possible positions Alice could take.
I think what people really find frustrating about moving goalposts is that they want their opponent to definitively lose. Bob wants Alice to publicly admit complete defeat. But instead of admitting defeat, Alice merely decides to replace her old claim with a new, slightly different one. But I would say that the desire for a clear surrender is an emotional one. In a way, Alice has admitted defeat by discarding her old position. She just hasn't done it loudly or theatrically. They seem to fantasize about their opponents saying, "I was a fool, and you are wise." Take what you can get, I say. The real goal of debate isn't victory, it's truth.
Rather than just talking about Alice and Bob, allow me to substitute a real life example. Many people think of "Intelligent Design" as being Creationism with a moved goalpost. Well, I think that means you can't always use the same arguments against the two. On the one hand, you could argue against both ID and Creationism by pointing out that Evolution is really one of the best established theories in all of science. On the other hand, you couldn't argue against ID by pointing out evidence of a 4.6 billion year history, because (as far as I know) ID already accepts the age of Earth. ID has a ton of problems, but it's still a slight step above Creationism. I just don't see the goalpost-moving as being in itself fallacious. Are people not allowed to change their minds, to improve their own positions?
Well, I guess in this case it's reasonable to want a definitive loss, but that's only because ID isn't so much a real debate as it is a silly PR machine.
*In case it isn't clear, Alice and Bob are just two names I am using to represent any two people in a debate. Physicists seem to be fond of using these two particular names in thought experiments, so I will do the same.
Friday, November 16, 2007
Special Relativity Part 3: Mass-energy
Part 0: More historical background
Part 1: The problem
Part 2: Space-Time
One of the results of SR is that velocities do not add. If one rocket is going to my right at 3/4 the speed of light, and another is going to my left at 3/4 the speed of light, these two speeds to not sum to 3/2 the speed of light. Instead, each rocket observes the other to be going at 24/25 the speed of light. The equation for the relativistic "sum" of two speeds is as follows:
(v1 + v2)/(1 + v1v2/c2)
...where v1 and v2 are the two speeds, and c is the speed of light
The derivation of this equation unfortunately relies on math that I skipped, so you'll have to take my word for it. It basically arises from the equations that fully describe lorentz contraction and time dilation. One thing to note is that if either v1 or v2 is equal to c, then the relativistic sum is equal to c. That means that no matter how fast an observer is moving, light will still travel at speed c. Einstein originally set out to explain why light is always observed to move at speed c, and now we've done it.
Also note that if v1 and v2 are both less than c, their relativistic sum will be less than c. So no matter how much you try, you can never push an object above speed c. In fact, what happens, is that the closer its speed is to c, the harder and harder it becomes to increase its speed. That means that Newton's second law (Force equals mass times acceleration) is wrong. At high speeds, it takes greater force for a smaller amount of acceleration. In some sense, the mass of the object increases when it speeds up. Specifically, the "relativistic mass" of the object increases. Usually when physicists talk about mass, by default they refer to "rest mass" (the mass of an object when it isn't moving) rather than the relativistic mass. The rest mass stays constant during acceleration.
Whenever you apply force to a moving object, you are transferring energy. You are also changing the object's relativistic mass. With a bit of calculus, we can conclude that energy is relativistic mass multiplied by a factor of c2. That's where we get the equation E=mc2.
Technically, the famous equation is incorrect. The correct form is E=ɣmc2, since these days, relativistic mass is written as ɣm. The letter m represents the rest mass of the object, though in Einstein's time, it was used to represent the relativistic mass, thus the source of this confusion. The number ɣ (represented by the letter gamma) is called the Lorentz factor, and it turns up in the equations for Lorentz contraction and time dilation. For the interested reader, ɣ=1/sqrt(1-v2/c2).
For a non-moving object, ɣ=1, but when the object's speed approaches light, ɣ approaches infinity. That means that E=mc2 is only true for an object that is not moving. In order to push an object to the speed of light, it would require an infinite amount of energy, and the object would gain an infinite amount of mass. Along with time-travel, this is why the speed of light is the ultimate speed limit. (However, this does not disprove the existence of tachyons, which, in theory, already start out faster than light, so that there is no need to push them through the light-speed barrier.)
I don't think most people realize the implications of this equation, so I want to expound upon them. Most people have heard that this is how atom bombs work. When an atom bomb explodes, the nuclei of Uranium atoms split apart. The way they split is such that the total mass decreases. Because c2 is such a large number, a small difference in mass results in a huge amount of energy. The same basic idea is behind hydrogen bombs, and nuclear power plants.
What most people don't realize is that mass-energy equivalence is true of all energy. If you use energy to heat up an object, it becomes a tiny bit heavier. This should not be surprising, since the temperature of an object tells you how fast the individual particles are moving, and I've already said that objects moving at higher speeds become more massive. But more surprising is that if you compress a spring, giving it potential energy, it becomes heavier. If you snap your fingers, you become slightly lighter, since a small amount of energy is released through the snapping sound.
Mind you, none of these mass differences come in large enough quantities that we would ever notice them, and they would be completely swamped by other effects. But mass-energy equivalence also gives protons and neutrons the vast majority of their mass. Without it, atoms would be too light, the force of gravity would be less effective, and we probably wouldn't exist. It is by the grace of Special Relativity (along with a ton of other cool physics) that we're all here.
This concludes my series on Special Relativity, though I may still talk about it, and go off on other tangents. If you've got any questions, ask, and I could write more to explain the answers.
Part 1: The problem
Part 2: Space-Time
One of the results of SR is that velocities do not add. If one rocket is going to my right at 3/4 the speed of light, and another is going to my left at 3/4 the speed of light, these two speeds to not sum to 3/2 the speed of light. Instead, each rocket observes the other to be going at 24/25 the speed of light. The equation for the relativistic "sum" of two speeds is as follows:
(v1 + v2)/(1 + v1v2/c2)
...where v1 and v2 are the two speeds, and c is the speed of light
The derivation of this equation unfortunately relies on math that I skipped, so you'll have to take my word for it. It basically arises from the equations that fully describe lorentz contraction and time dilation. One thing to note is that if either v1 or v2 is equal to c, then the relativistic sum is equal to c. That means that no matter how fast an observer is moving, light will still travel at speed c. Einstein originally set out to explain why light is always observed to move at speed c, and now we've done it.
Also note that if v1 and v2 are both less than c, their relativistic sum will be less than c. So no matter how much you try, you can never push an object above speed c. In fact, what happens, is that the closer its speed is to c, the harder and harder it becomes to increase its speed. That means that Newton's second law (Force equals mass times acceleration) is wrong. At high speeds, it takes greater force for a smaller amount of acceleration. In some sense, the mass of the object increases when it speeds up. Specifically, the "relativistic mass" of the object increases. Usually when physicists talk about mass, by default they refer to "rest mass" (the mass of an object when it isn't moving) rather than the relativistic mass. The rest mass stays constant during acceleration.
Whenever you apply force to a moving object, you are transferring energy. You are also changing the object's relativistic mass. With a bit of calculus, we can conclude that energy is relativistic mass multiplied by a factor of c2. That's where we get the equation E=mc2.
Technically, the famous equation is incorrect. The correct form is E=ɣmc2, since these days, relativistic mass is written as ɣm. The letter m represents the rest mass of the object, though in Einstein's time, it was used to represent the relativistic mass, thus the source of this confusion. The number ɣ (represented by the letter gamma) is called the Lorentz factor, and it turns up in the equations for Lorentz contraction and time dilation. For the interested reader, ɣ=1/sqrt(1-v2/c2).
For a non-moving object, ɣ=1, but when the object's speed approaches light, ɣ approaches infinity. That means that E=mc2 is only true for an object that is not moving. In order to push an object to the speed of light, it would require an infinite amount of energy, and the object would gain an infinite amount of mass. Along with time-travel, this is why the speed of light is the ultimate speed limit. (However, this does not disprove the existence of tachyons, which, in theory, already start out faster than light, so that there is no need to push them through the light-speed barrier.)
I don't think most people realize the implications of this equation, so I want to expound upon them. Most people have heard that this is how atom bombs work. When an atom bomb explodes, the nuclei of Uranium atoms split apart. The way they split is such that the total mass decreases. Because c2 is such a large number, a small difference in mass results in a huge amount of energy. The same basic idea is behind hydrogen bombs, and nuclear power plants.
What most people don't realize is that mass-energy equivalence is true of all energy. If you use energy to heat up an object, it becomes a tiny bit heavier. This should not be surprising, since the temperature of an object tells you how fast the individual particles are moving, and I've already said that objects moving at higher speeds become more massive. But more surprising is that if you compress a spring, giving it potential energy, it becomes heavier. If you snap your fingers, you become slightly lighter, since a small amount of energy is released through the snapping sound.
Mind you, none of these mass differences come in large enough quantities that we would ever notice them, and they would be completely swamped by other effects. But mass-energy equivalence also gives protons and neutrons the vast majority of their mass. Without it, atoms would be too light, the force of gravity would be less effective, and we probably wouldn't exist. It is by the grace of Special Relativity (along with a ton of other cool physics) that we're all here.
This concludes my series on Special Relativity, though I may still talk about it, and go off on other tangents. If you've got any questions, ask, and I could write more to explain the answers.
Atheist Blogroll added
I've added, and been added to the Atheist Blogroll, which is organized by Mojoey of Deep Thoughts. It has almost 500 blogs. To be honest, I signed up because of this cool video from toomanytribbles. I like the music. I'm told it's Battlestar Galactica.
Thursday, November 15, 2007
Nica Lalli visits
Last night, the campus nontheist group got Nica Lalli to come over for a talk and dinner. Nica Lalli is an art educator from Brooklyn, and the author of Nothing: Something to Believe in.
 So Nica is one of those "friendly" types who isn't so interested in trying to argue for or against a god, but rather in getting on with life. Many people, including atheists, think Dawkins, Harris, and Hitchens (the unholy trinity) focus too much on just religious criticism. There is a role for such criticism, but we also need books to put a human face on the movement. Well, now we have at least one such a book, thanks to Nica. In contrast with other popular atheist books, Nothing is not about criticizing religion, but about her personal story of how she grew up without religion.
So Nica is one of those "friendly" types who isn't so interested in trying to argue for or against a god, but rather in getting on with life. Many people, including atheists, think Dawkins, Harris, and Hitchens (the unholy trinity) focus too much on just religious criticism. There is a role for such criticism, but we also need books to put a human face on the movement. Well, now we have at least one such a book, thanks to Nica. In contrast with other popular atheist books, Nothing is not about criticizing religion, but about her personal story of how she grew up without religion.
Nica prefers the word "nothing" to all the other labels. She thinks that we should actually get to know people first, before labeling and putting them into separate boxes. I really sympathize with this. Why, just the other day, a friend of mine was making a bunch of off-hand comments on how several things I said were the "skeptical" things to say. Something about that attitude was a little irritating. I don't think the way I do just because I'm a skeptic--it's the other way around! Freethinkers have a real mess of identity politics. Every word seems to have a ton of hidden meanings. On the other hand, (and here comes some very light criticism) I think part of the problem is also that freethinkers seem to be awfully fond of creating whole new words that further divide, as Nica does too with "nothing." But then, I would have trouble arguing that "nothing" is at all divisive.
Anyways, meeting her was pretty cool, because she's the first "celebrity" I've met. Well, Dan Barker came by a few weeks ago, but I had to leave right after the talk. I read about these people, but I never expect to meet them myself. She was very down-to-earth. We talked about art, the weather, and food, as well as objectivism, animal rights, and creationism. She was interested in meeting college atheist activist groups, which didn't exist in her time. I'm not, strictly speaking, a member of the local group, so I was sort of meeting them at the time as she.
 So Nica is one of those "friendly" types who isn't so interested in trying to argue for or against a god, but rather in getting on with life. Many people, including atheists, think Dawkins, Harris, and Hitchens (the unholy trinity) focus too much on just religious criticism. There is a role for such criticism, but we also need books to put a human face on the movement. Well, now we have at least one such a book, thanks to Nica. In contrast with other popular atheist books, Nothing is not about criticizing religion, but about her personal story of how she grew up without religion.
So Nica is one of those "friendly" types who isn't so interested in trying to argue for or against a god, but rather in getting on with life. Many people, including atheists, think Dawkins, Harris, and Hitchens (the unholy trinity) focus too much on just religious criticism. There is a role for such criticism, but we also need books to put a human face on the movement. Well, now we have at least one such a book, thanks to Nica. In contrast with other popular atheist books, Nothing is not about criticizing religion, but about her personal story of how she grew up without religion.Nica prefers the word "nothing" to all the other labels. She thinks that we should actually get to know people first, before labeling and putting them into separate boxes. I really sympathize with this. Why, just the other day, a friend of mine was making a bunch of off-hand comments on how several things I said were the "skeptical" things to say. Something about that attitude was a little irritating. I don't think the way I do just because I'm a skeptic--it's the other way around! Freethinkers have a real mess of identity politics. Every word seems to have a ton of hidden meanings. On the other hand, (and here comes some very light criticism) I think part of the problem is also that freethinkers seem to be awfully fond of creating whole new words that further divide, as Nica does too with "nothing." But then, I would have trouble arguing that "nothing" is at all divisive.
Anyways, meeting her was pretty cool, because she's the first "celebrity" I've met. Well, Dan Barker came by a few weeks ago, but I had to leave right after the talk. I read about these people, but I never expect to meet them myself. She was very down-to-earth. We talked about art, the weather, and food, as well as objectivism, animal rights, and creationism. She was interested in meeting college atheist activist groups, which didn't exist in her time. I'm not, strictly speaking, a member of the local group, so I was sort of meeting them at the time as she.
Wednesday, November 14, 2007
Bad science: homeopathy
As promised, it's time to debunk homeopathy. Homeopathy is a type of "medicine" that originated early 19th century. Perhaps at the time, homeopathy might have made sense, and may even have been safer than other practices of the time. But with today's knowledge, homeopathy is clearly based on false premises. Homeopathy cannot possibly work, nor does it. The fact that homeopathy is accepted as alternative medicine, I think, casts serious doubt on all alternative medicine. If so-called "alternative" medicine cannot distinguish between practices that just might work if we thoroughly tested them (ie herbal medicines) and practices like homeopathy, which cannot possibly work, then it is worthless.
So what is homeopathy? Homeopathy is based on the idea that like cures like. In other words, if you have a cough, you take something that causes coughs. The idea is that everything has a potential to cause symptoms and to cure them. Obviously, we would only want the curing potential. Homeopathy solves this by a process of dilution. The more the remedy is diluted, the greater its curing effect, and the lesser its negative symptoms.
Every step of the way, this simply does not make sense. Why in the world should like cure like? Sure, that's how vaccines seem to work, but that's because vaccines work with the immune system. Homeopathy has no such rationale. In fact, homeopathy does not even deal with the sources of disease, like bacteria, or viruses, and so forth. Homeopathy only looks at the symptoms. So like cures like, even when the two likes have completely different causes.
And the dilution! By homeopathic logic, things become stronger when you dilute them. So if you drop a tiny bit of medicine into the ocean, you might kill all the fish with an overdose. That means that if you accidentally contaminated the ocean with a single drop, you should put in a couple more tons of the stuff in to keep it from getting too dilute. Oh, but I guess they say dilution only increases the strength of the good effects, and not the bad ones. Isn't it lucky that these little molecules are able to distinguish good and evil?
As a matter of fact, typical homeopathic medicine has been diluted so much to the extent that there is no longer any of the original medicine. Early homeopaths obviously did not know about Avogadro's number. At normal sizes, any dose of medicine consists of on the order of 10^23 molecules in it. If you dilute this, you will reduce the number of molecules in the dose. Let's say that the number of molecules is reduced by a factor of 10 for each dilution. After 23 of these dilutions, you'll have on average one molecule in the solution. As if that weren't enough, the medicine is diluted even more. You can't have a fraction of a molecule left over, so the end result is that it's extremely likely that there is not a single molecule left. All you have is water.
But let's not attack a straw man here. I'm leaving out one supposedly important detail. At each step of the dilution, the solution undergoes a process called succussion. This involves shaking the solution vigorously, which I guess releases the spirits from it or something. Modern homeopaths would say that this impresses upon the water a "memory" of the chemical. I would have thought that any structures in the liquid would be destroyed by the slightest shaking. Even if you could create stable structures in liquid water, whatever reason is there to think the water's "memory" would have the same effects as the original medication? Homeopathy is basically postulating magic water.
But if so many educated people believe homeopathy is effective, surely there must be at least a little truth to the claims, right? Well, no. The first thing that you learn from skepticism is that there are countless cases in which the masses have fooled themselves. People tend to rely on anecdotal evidence rather than experimental evidence. They say, "It may not make sense to the scientists, but I've still seen it work for a lot of people." But anecdotal evidence is extremely vulnerable to confirmation bias and small sampling errors.
Another problem is that people underestimate the placebo effect. A placebo is basically a sugar pill that misleads people into thinking that they have taken real medicine. When comparing people who have taken a placebo and people who have taken nothing, the placebo group tends to do better. This is called the placebo effect. Homeopathy is essentially a placebo, except it's made of magic water instead of a sugar pill. To filter out the placebo effect, experiments must compare the effects of a medicine with the effects of a placebo. This is impossible to do with anecdotes. All the apparent good effects of homeopathy, if any, are basically a result of the placebo effect.
I hear that homeopaths tend to be really nice people who give their patients ample attention, which in itself may be good for the patients' health. Now if only those homeopaths would add real medicine to their practice, rather than magic.
For further reading (also, information on studies disproving homeopathy), I recommend the Skeptic's Dictionary.
So what is homeopathy? Homeopathy is based on the idea that like cures like. In other words, if you have a cough, you take something that causes coughs. The idea is that everything has a potential to cause symptoms and to cure them. Obviously, we would only want the curing potential. Homeopathy solves this by a process of dilution. The more the remedy is diluted, the greater its curing effect, and the lesser its negative symptoms.
Every step of the way, this simply does not make sense. Why in the world should like cure like? Sure, that's how vaccines seem to work, but that's because vaccines work with the immune system. Homeopathy has no such rationale. In fact, homeopathy does not even deal with the sources of disease, like bacteria, or viruses, and so forth. Homeopathy only looks at the symptoms. So like cures like, even when the two likes have completely different causes.
And the dilution! By homeopathic logic, things become stronger when you dilute them. So if you drop a tiny bit of medicine into the ocean, you might kill all the fish with an overdose. That means that if you accidentally contaminated the ocean with a single drop, you should put in a couple more tons of the stuff in to keep it from getting too dilute. Oh, but I guess they say dilution only increases the strength of the good effects, and not the bad ones. Isn't it lucky that these little molecules are able to distinguish good and evil?
As a matter of fact, typical homeopathic medicine has been diluted so much to the extent that there is no longer any of the original medicine. Early homeopaths obviously did not know about Avogadro's number. At normal sizes, any dose of medicine consists of on the order of 10^23 molecules in it. If you dilute this, you will reduce the number of molecules in the dose. Let's say that the number of molecules is reduced by a factor of 10 for each dilution. After 23 of these dilutions, you'll have on average one molecule in the solution. As if that weren't enough, the medicine is diluted even more. You can't have a fraction of a molecule left over, so the end result is that it's extremely likely that there is not a single molecule left. All you have is water.
But let's not attack a straw man here. I'm leaving out one supposedly important detail. At each step of the dilution, the solution undergoes a process called succussion. This involves shaking the solution vigorously, which I guess releases the spirits from it or something. Modern homeopaths would say that this impresses upon the water a "memory" of the chemical. I would have thought that any structures in the liquid would be destroyed by the slightest shaking. Even if you could create stable structures in liquid water, whatever reason is there to think the water's "memory" would have the same effects as the original medication? Homeopathy is basically postulating magic water.
But if so many educated people believe homeopathy is effective, surely there must be at least a little truth to the claims, right? Well, no. The first thing that you learn from skepticism is that there are countless cases in which the masses have fooled themselves. People tend to rely on anecdotal evidence rather than experimental evidence. They say, "It may not make sense to the scientists, but I've still seen it work for a lot of people." But anecdotal evidence is extremely vulnerable to confirmation bias and small sampling errors.
Another problem is that people underestimate the placebo effect. A placebo is basically a sugar pill that misleads people into thinking that they have taken real medicine. When comparing people who have taken a placebo and people who have taken nothing, the placebo group tends to do better. This is called the placebo effect. Homeopathy is essentially a placebo, except it's made of magic water instead of a sugar pill. To filter out the placebo effect, experiments must compare the effects of a medicine with the effects of a placebo. This is impossible to do with anecdotes. All the apparent good effects of homeopathy, if any, are basically a result of the placebo effect.
I hear that homeopaths tend to be really nice people who give their patients ample attention, which in itself may be good for the patients' health. Now if only those homeopaths would add real medicine to their practice, rather than magic.
For further reading (also, information on studies disproving homeopathy), I recommend the Skeptic's Dictionary.
Tuesday, November 13, 2007
Little brother blogger
It seems my little brother, who is in 8th grade, has gone ahead and started his own blog. I don't know what to say. When I was his age, I didn't look at the internet. Who knows what nefarious things he is planning?
But I'm not going to dwell on it, since contrary to current appearances, my blog is not about my family, nor is it exclusively for my family. The internet does not need to hear about my family.
But I'm not going to dwell on it, since contrary to current appearances, my blog is not about my family, nor is it exclusively for my family. The internet does not need to hear about my family.
To friends and family
It has come to my attention that certain close relatives will inevitably find this blog. Well, I knew this would happen from the start. I have made no effort to hide the fact that I have a blog (it's on facebook, and I have mentioned it in conversation more than once). A year ago, I would have had reservations about talking about my atheism, but I no longer care if people know. I now realize that any fears were of my own making.
First, a little background. I consider myself to have deconverted somewhere between my junior year of high school and high school graduation. Previous to that, I didn't think too much about it. I went to a Catholic, Jesuit high school. I still think highly of the school, the education, and the Jesuits. I give them a lot of credit. I am not atheist because of a lack of education. I simply insisted on thinking for myself, as should all.
I say all this to disperse any feelings that anyone is "to blame". But the other reason that no one is "to blame" is that I don't even see it as a bad thing. For someone of my background, being atheist makes hardly a difference in who I really am. I would have the same personality, interests, and behaviors. Would it really make much of a difference if, in my long blog posts plumbing the depths of philosophy, I came to a slightly different conclusion at the end? I don't think anyone would ever have noticed if I never said anything about it. No, nothing happens to my morality either. For a college student, the morals I have are relatively conservative (e.g. no alcohol). If my beliefs have made no difference in how I act, and will never do so, why should a god, or anyone, take offense to them?
Another thing I should say is that I do not consider myself to be a "seeker". I do not consider this to be one step in a spiritual journey. No, I think that this was just one brief detour, ended long ago, in the larger journey of life, which, when it comes down to it, really isn't just about religion.
First, a little background. I consider myself to have deconverted somewhere between my junior year of high school and high school graduation. Previous to that, I didn't think too much about it. I went to a Catholic, Jesuit high school. I still think highly of the school, the education, and the Jesuits. I give them a lot of credit. I am not atheist because of a lack of education. I simply insisted on thinking for myself, as should all.
I say all this to disperse any feelings that anyone is "to blame". But the other reason that no one is "to blame" is that I don't even see it as a bad thing. For someone of my background, being atheist makes hardly a difference in who I really am. I would have the same personality, interests, and behaviors. Would it really make much of a difference if, in my long blog posts plumbing the depths of philosophy, I came to a slightly different conclusion at the end? I don't think anyone would ever have noticed if I never said anything about it. No, nothing happens to my morality either. For a college student, the morals I have are relatively conservative (e.g. no alcohol). If my beliefs have made no difference in how I act, and will never do so, why should a god, or anyone, take offense to them?
Another thing I should say is that I do not consider myself to be a "seeker". I do not consider this to be one step in a spiritual journey. No, I think that this was just one brief detour, ended long ago, in the larger journey of life, which, when it comes down to it, really isn't just about religion.
Monday, November 12, 2007
Miscellaneous blogging issues
Ok, I have a few blogging questions. I'm not posing them to anyone in particular, they just happen to be on my mind.
One of the things that really annoys me is that whenever I post something, the default time stamp is set to the time that I started writing the draft. This makes no sense. I want the time stamp to be the time when I actually post the item. If I don't change it manually every time, my post ends up looking several days old, and won't appear on the top. What is up with Blogger and its bugs?
Another problem is that there is no easy way to have a "fold" in my posts. On most blogs, the author can choose to show only the first paragraph or so of a post so that readers who want more can click on a link to get the full article. I found a complicated hack that can do this, but it had a small bug, and I decided it wasn't worthwhile.
Another issue is my blog title and tagline. I don't exactly know why I picked the title "Skeptic's Play". I guess I have this vague notion in my mind that the title signifies that I focus more on "fun" skepticism as opposed to "serious" skepticism. "Fun" skepticism is talking about abstract ideas that branch wildly from science and skepticism (obviously, not everyone's idea of fun). "Serious" skepticism is actually doing serious research on pseudoscientific claims (can be fun too, but it's hard work). At least, those were the thoughts that went through my mind when I rather quickly picked a title.
I have every intention of sticking with the title, but I do want a more descriptive and/or clever tagline that maybe explains my blog and its title. I am having trouble thinking anything up because, title aside, it is not clear to me what the focus of my blog really is. I just talk about what interests me.
It reminds me of one of Louis Sachar's Wayside School stories. In it, there was a lot of ice cream, each scoop flavored like a different one of the students. Whenever a student tasted another student's ice cream, the taste represented what they thought of that student. Whenever a student tasted his or her own ice cream, it was flavorless. Basically what I'm saying is that if my blog were an ice cream flavor, I wouldn't be able to taste it.
On a related note, I realize that there is no way to contact me outside of comments. I could create a new e-mail address, but I will only do so if there is enough demand for it.
One of the things that really annoys me is that whenever I post something, the default time stamp is set to the time that I started writing the draft. This makes no sense. I want the time stamp to be the time when I actually post the item. If I don't change it manually every time, my post ends up looking several days old, and won't appear on the top. What is up with Blogger and its bugs?
Another problem is that there is no easy way to have a "fold" in my posts. On most blogs, the author can choose to show only the first paragraph or so of a post so that readers who want more can click on a link to get the full article. I found a complicated hack that can do this, but it had a small bug, and I decided it wasn't worthwhile.
Another issue is my blog title and tagline. I don't exactly know why I picked the title "Skeptic's Play". I guess I have this vague notion in my mind that the title signifies that I focus more on "fun" skepticism as opposed to "serious" skepticism. "Fun" skepticism is talking about abstract ideas that branch wildly from science and skepticism (obviously, not everyone's idea of fun). "Serious" skepticism is actually doing serious research on pseudoscientific claims (can be fun too, but it's hard work). At least, those were the thoughts that went through my mind when I rather quickly picked a title.
I have every intention of sticking with the title, but I do want a more descriptive and/or clever tagline that maybe explains my blog and its title. I am having trouble thinking anything up because, title aside, it is not clear to me what the focus of my blog really is. I just talk about what interests me.
It reminds me of one of Louis Sachar's Wayside School stories. In it, there was a lot of ice cream, each scoop flavored like a different one of the students. Whenever a student tasted another student's ice cream, the taste represented what they thought of that student. Whenever a student tasted his or her own ice cream, it was flavorless. Basically what I'm saying is that if my blog were an ice cream flavor, I wouldn't be able to taste it.
On a related note, I realize that there is no way to contact me outside of comments. I could create a new e-mail address, but I will only do so if there is enough demand for it.
Sunday, November 11, 2007
Blocks and Towers solution
See the puzzle
Let's say that you've found every single way to build a 1x10 tower. Imagine that you've lined up each of these solutions. Let's remove the top block from each 1x10 tower. For some of them, you will be removing a 1x2 block, and for others, you will be removing a 1x1 block. You will be left with a bunch of 1x8 towers and 1x9 towers.
But here's the crucial point. The 1x8 and 1x9 towers constitute the complete set of solutions for towers of those sizes. No matter what kind of 1x8 tower you can build, you can always add a 1x2 block on top to get a unique 1x10 tower. Similarly, you can always add a 1x1 block on top of a 1x9 tower. Therefore, the total number of unique 1x10 towers you can build is equal to the sum of the total number of 1x8 towers and 1x9 towers.
In fact, this isn't just true of 1x10 towers. The number of ways to build any 1xN tower is equal to the sum of the ways to build 1x(N-1) and 1x(N-2) towers. So if we start with 1x1 towers (1 way) and 1x2 towers (2 ways), we can proceed to calculate the total number of ways for any size of tower:
1x1: 1
1x2: 2
1x3: 3
1x4: 5
1x5: 8
1x6: 13
1x7: 21
1x8: 34
1x9: 55
1x10: 89
This sequence of numbers is known as the Fibonacci sequence. I actually mentioned this sequence not-so-subtly in a previous post, and was even kind enough to give a closed expression for it. The number of ways to build a 1xN tower is equal to F(N+1).
The Fibonacci sequence is one of those things that seems to show up everywhere. It is closely related to the number called "the golden ratio", which I'm sure most people have heard about. It turns up all the time in nature.
Let's say that you've found every single way to build a 1x10 tower. Imagine that you've lined up each of these solutions. Let's remove the top block from each 1x10 tower. For some of them, you will be removing a 1x2 block, and for others, you will be removing a 1x1 block. You will be left with a bunch of 1x8 towers and 1x9 towers.
But here's the crucial point. The 1x8 and 1x9 towers constitute the complete set of solutions for towers of those sizes. No matter what kind of 1x8 tower you can build, you can always add a 1x2 block on top to get a unique 1x10 tower. Similarly, you can always add a 1x1 block on top of a 1x9 tower. Therefore, the total number of unique 1x10 towers you can build is equal to the sum of the total number of 1x8 towers and 1x9 towers.
In fact, this isn't just true of 1x10 towers. The number of ways to build any 1xN tower is equal to the sum of the ways to build 1x(N-1) and 1x(N-2) towers. So if we start with 1x1 towers (1 way) and 1x2 towers (2 ways), we can proceed to calculate the total number of ways for any size of tower:
1x1: 1
1x2: 2
1x3: 3
1x4: 5
1x5: 8
1x6: 13
1x7: 21
1x8: 34
1x9: 55
1x10: 89
This sequence of numbers is known as the Fibonacci sequence. I actually mentioned this sequence not-so-subtly in a previous post, and was even kind enough to give a closed expression for it. The number of ways to build a 1xN tower is equal to F(N+1).
The Fibonacci sequence is one of those things that seems to show up everywhere. It is closely related to the number called "the golden ratio", which I'm sure most people have heard about. It turns up all the time in nature.
Carnival of the Godless #79
Right now, the Carnival of the Godless #79 is up at Aardvarchaeology. It features my own post Hell vs Altruism, among a ton of other articles from the godless part of the blogosphere.
Also, the Skeptics' Circle #73 is up at Holford Watch. Go read it.
Also, the Skeptics' Circle #73 is up at Holford Watch. Go read it.
Saturday, November 10, 2007
Anthony Flew and other conversions
The buzz in the atheist blogosphere is about Antony Flew, a "notorious atheist" who has converted to deism and published a book. Here's an NYT article, a response by Richard Carrier, a person involved, and PZ's comment on the matter.
The title of the book, There is a God: How the World's Most Notorious Atheist Changed his Mind, is a bit of a distortion. One of the things you learn from the blogosphere is the names of all the important activists and other people involved in the movement. But I've never heard of Antony Flew, so he's hardly notorious. Apparently, he used to be well-known in philosophy circles. Currently, he seems to be aging badly, and losing his memory (Flew himself says he has "nominal aphasia"). The book, as Richard Carrier will tell you, is transparently the work of Christian apologists putting words into Flew's mouth with the purpose of using his "authority", as if he had any. It's all rather appalling. Talk about liars for Jesus.
I think we can all agree that this is reprehensible, so moving on... there is another issue. Now, I'd like to think that people really can rationally disagree in a debate even when they agree on the facts. Your typical debate is often extremely complex underneath the surface, so it's completely natural for people to disagree, at least on the details. I'd like to think that people are capable of changing their mind rationally, and by their own choice.
But, wow, examples like these sure make it difficult to make my case. Where are all the clear-minded conversions from atheism to theism? Here, Antony is clearly suffering from memory loss and muddled thinking, and he hasn't even bothered to look closely at the book under his own name. And this only got him as far as deism, which is hardly any closer to Christianity than is atheism. Another example is Francis Collins, the famous Christian scientist, and author of The Language of God. Collins shows every sign of having gone through the conversion emotionally and not rationally. Take this quote:
What I'm saying is that I want to be humble. I want to see intelligent people rationally disagreeing with me. I want to see that people who convert can do so rationally. It's a sign of freedom of thought. And my faith in humanity sort of depends on it. The alternative, after all, is that large swaths of the population are completely irrational in most respects. Perhaps I am just looking in the wrong places. The looming cynicism is clouding my judgement...
The title of the book, There is a God: How the World's Most Notorious Atheist Changed his Mind, is a bit of a distortion. One of the things you learn from the blogosphere is the names of all the important activists and other people involved in the movement. But I've never heard of Antony Flew, so he's hardly notorious. Apparently, he used to be well-known in philosophy circles. Currently, he seems to be aging badly, and losing his memory (Flew himself says he has "nominal aphasia"). The book, as Richard Carrier will tell you, is transparently the work of Christian apologists putting words into Flew's mouth with the purpose of using his "authority", as if he had any. It's all rather appalling. Talk about liars for Jesus.
I think we can all agree that this is reprehensible, so moving on... there is another issue. Now, I'd like to think that people really can rationally disagree in a debate even when they agree on the facts. Your typical debate is often extremely complex underneath the surface, so it's completely natural for people to disagree, at least on the details. I'd like to think that people are capable of changing their mind rationally, and by their own choice.
But, wow, examples like these sure make it difficult to make my case. Where are all the clear-minded conversions from atheism to theism? Here, Antony is clearly suffering from memory loss and muddled thinking, and he hasn't even bothered to look closely at the book under his own name. And this only got him as far as deism, which is hardly any closer to Christianity than is atheism. Another example is Francis Collins, the famous Christian scientist, and author of The Language of God. Collins shows every sign of having gone through the conversion emotionally and not rationally. Take this quote:
Nobody gets argued all the way into becoming a believer on the sheer basis of logic and reason. That requires a leap of faith. And that leap of faith seemed very scary to me. After I had struggled with this for a couple of years, I was hiking in the Cascade Mountains on a beautiful fall afternoon. I turned the corner and saw in front of me this frozen waterfall, a couple of hundred feet high. Actually, a waterfall that had three parts to it -- also the symbolic three in one. At that moment, I felt my resistance leave me. And it was a great sense of relief. The next morning, in the dewy grass in the shadow of the Cascades, I fell on my knees and accepted this truth -- that God is God, that Christ is his son and that I am giving my life to that belief.As PZ said,
If it had been a two part waterfall, would he have converted to Zoroastrianism?And of course, you hear people all the time who say "I used to be an atheist," but are now, like, devout Christians or something. For example, Kirk Cameron, one of the apologists responsible for the "banana argument", claims that he used to be an atheist. Well, if so, he obviously wasn't a very well-informed one. It would be an insult to the rest of humanity not to point out how woefully ignorant Kirk is.
What I'm saying is that I want to be humble. I want to see intelligent people rationally disagreeing with me. I want to see that people who convert can do so rationally. It's a sign of freedom of thought. And my faith in humanity sort of depends on it. The alternative, after all, is that large swaths of the population are completely irrational in most respects. Perhaps I am just looking in the wrong places. The looming cynicism is clouding my judgement...
Friday, November 9, 2007
"Extraordinary claims" defined
"Extraordinary claims require extraordinary evidence." This is a skeptical maxim, usually credited to Sagan (though others have said similar things before him). Basically what this means is that if you make increasingly fantastic claims, the skeptic is not increasingly impressed, but rather wants more evidence. But sometimes, there is confusion about this saying. What constitutes an "extraordinary claim"? And is the saying always true, or a rule of thumb?
There are several ways to define extraordinary claims. The most obvious definition would be those claims that require extraordinary evidence. That makes our maxim into a nice tautology; it is guaranteed to be true. But the problem with tautologies is that they do not tell us much. How do we tell an extraordinary claim from an ordinary one? We look to see whether it requires extraordinary evidence. How do we know whether it requires extraordinary evidence? We look to see whether it is an extraordinary claim. All in all, this is a useless definition.
There is another obvious definition that is not tautologous. An extraordinary claim is one that is already contradicted by extraordinary evidence. Under this definition, our maxim basically says that the only way to counter evidence is with more evidence. I think that this is self-evidently true, and quite useful. For an example application, take astrology. There are no known forces that might cause planets to affect our destinies, none that act even remotely similarly. Add to that the numerous studies that have shown astrology ineffective, and we've got quite an extraordinary claim here.
However, I think that skeptics usually mean much more by "extraordinary claims". The qualities that can make a claim extraordinary aren't completely arbitrary, but I would still have difficulty describing them. I would say that beyond this point, the maxim changes from an absolute truth to a rule of thumb.
The first, perhaps most important quality that can make a claim extraordinary is if it is unnecessarily complicated. This principle is called Occam's Razor, and it really deserves a separate discussion. Suffice it to say that inserting invisible unicorns into your theories usually does not improve them.
Another quality that makes a claim extraordinary is if it has important implications. If accepting a claim is a matter of life and death, you better be sure to supply lots of evidence. The caveat is that this often works both ways. For example, if I claim that children's vaccines are causing autism, this really is a matter of life and death, since vaccines save lives and autism harms them. However, the counter-claim that vaccines are not causing autism is also a matter of life and death. Both of these are extraordinary claims, but we obviously have to choose one, regardless of how little evidence we have. (In this case, the evidence says that vaccines do not cause autism.)
There are more qualities, but at this point it becomes difficult to pick them out. In reality, most skeptics just have an intuitive notion of what sort of claims are sensible and what sort are ridiculous. You know it when you see it. But I think skeptics would do better to try to explain a rationale for what makes claims extraordinary--which is what I just did.
There are several ways to define extraordinary claims. The most obvious definition would be those claims that require extraordinary evidence. That makes our maxim into a nice tautology; it is guaranteed to be true. But the problem with tautologies is that they do not tell us much. How do we tell an extraordinary claim from an ordinary one? We look to see whether it requires extraordinary evidence. How do we know whether it requires extraordinary evidence? We look to see whether it is an extraordinary claim. All in all, this is a useless definition.
There is another obvious definition that is not tautologous. An extraordinary claim is one that is already contradicted by extraordinary evidence. Under this definition, our maxim basically says that the only way to counter evidence is with more evidence. I think that this is self-evidently true, and quite useful. For an example application, take astrology. There are no known forces that might cause planets to affect our destinies, none that act even remotely similarly. Add to that the numerous studies that have shown astrology ineffective, and we've got quite an extraordinary claim here.
However, I think that skeptics usually mean much more by "extraordinary claims". The qualities that can make a claim extraordinary aren't completely arbitrary, but I would still have difficulty describing them. I would say that beyond this point, the maxim changes from an absolute truth to a rule of thumb.
The first, perhaps most important quality that can make a claim extraordinary is if it is unnecessarily complicated. This principle is called Occam's Razor, and it really deserves a separate discussion. Suffice it to say that inserting invisible unicorns into your theories usually does not improve them.
Another quality that makes a claim extraordinary is if it has important implications. If accepting a claim is a matter of life and death, you better be sure to supply lots of evidence. The caveat is that this often works both ways. For example, if I claim that children's vaccines are causing autism, this really is a matter of life and death, since vaccines save lives and autism harms them. However, the counter-claim that vaccines are not causing autism is also a matter of life and death. Both of these are extraordinary claims, but we obviously have to choose one, regardless of how little evidence we have. (In this case, the evidence says that vaccines do not cause autism.)
There are more qualities, but at this point it becomes difficult to pick them out. In reality, most skeptics just have an intuitive notion of what sort of claims are sensible and what sort are ridiculous. You know it when you see it. But I think skeptics would do better to try to explain a rationale for what makes claims extraordinary--which is what I just did.
Thursday, November 8, 2007
Blocks and Towers
Difficulty: 5 of 10
One of my favorite kinds of puzzles involved a branch of mathematics called combinatorics. Combinatorics is basically all about counting things. Sounds easy, right? Good. I recommend sustaining this delusion as long as possible. I should also add that there are many practical applications to combinatorics. For example, we've been using combinatorics in my statistical physics class to calculate probabilities, which are then used to explain the behavior of large systems.
Here is an interesting combinatorics problem which doesn't require any knowledge of combinatorics, but does require a lot of cleverness. This is probably the hardest puzzle I've posted so far. You have an infinite number of 1x1 blocks and 1x2 blocks. You want to put some of them together so they make a tower of 1x10. How many different ways are there to do this?
To better understand the problem, first try smaller towers. I'm going to abbreviate each possible way into a string of 1s and 2s, representing a 1x1 blocks and a 1x2 blocks respectively. For a 1x1 tower, there is only one way: a single 1. For a 1x2 tower, there are two ways: 11 and 2. For 1x3, there are three ways: 111, 12, and 21. For 1x4, there are five ways: 1111, 211, 121, 112, and 22. Pretty soon, you'll need more than just your fingers to count these.
Ok, so I lied. I'm not just interested in 1x10 towers. I'm interested in any 1xN sized tower. A general formula, if possible, would be best. You might find a hint somewhere in my post explaining mathematical induction. (Is this puzzle the real reason I bothered with induction? I won't say!)
See the solution (Need I say, spoiler alert?)
One of my favorite kinds of puzzles involved a branch of mathematics called combinatorics. Combinatorics is basically all about counting things. Sounds easy, right? Good. I recommend sustaining this delusion as long as possible. I should also add that there are many practical applications to combinatorics. For example, we've been using combinatorics in my statistical physics class to calculate probabilities, which are then used to explain the behavior of large systems.
Here is an interesting combinatorics problem which doesn't require any knowledge of combinatorics, but does require a lot of cleverness. This is probably the hardest puzzle I've posted so far. You have an infinite number of 1x1 blocks and 1x2 blocks. You want to put some of them together so they make a tower of 1x10. How many different ways are there to do this?
To better understand the problem, first try smaller towers. I'm going to abbreviate each possible way into a string of 1s and 2s, representing a 1x1 blocks and a 1x2 blocks respectively. For a 1x1 tower, there is only one way: a single 1. For a 1x2 tower, there are two ways: 11 and 2. For 1x3, there are three ways: 111, 12, and 21. For 1x4, there are five ways: 1111, 211, 121, 112, and 22. Pretty soon, you'll need more than just your fingers to count these.
Ok, so I lied. I'm not just interested in 1x10 towers. I'm interested in any 1xN sized tower. A general formula, if possible, would be best. You might find a hint somewhere in my post explaining mathematical induction. (Is this puzzle the real reason I bothered with induction? I won't say!)
See the solution (Need I say, spoiler alert?)
Induction in mathematics
In mathematics, there is a type of proof called induction. This is not to be confused with inductive reasoning--this is an entirely different concept which just happens to have similar etymology.
So let's say I wanted to prove the below equation for all natural numbers n. (The natural number are {1, 2, 3, 4, 5, ... }.)
1 + 2 + 3 + ... + n = n*(n+1)/2
First, let's test the equation for a few values of n.
1 = 1*(1+1)/2 = 1
1 + 2 = 2*(2+1)/2 = 3
1 + 2 + 3 = 3*(3+1)/2 = 6
1 + 2 + 3 + 4 = 4*(4+1)/2 = 10
So do you get the idea? But how do we prove that the equation is true for all n? There are infinite natural numbers, so we can't just go through them one by one.
What we use is a method called induction. First, we prove that the equation is true for n = 1. Second, we show that if it is true for n = k, it is also true for n = k+1. After we have proven this, we know that the equation is true for n = 1, and therefore n = 2, and therefore n = 3, and so on. The equation is true for n = {1, 2, 3, 4, 5, ...} = all natural numbers. It's that easy.
So here goes:
Step 1: 1 = 1*(1+1)/2 = 1
Step 2:
Assume: 1 + 2 + 3 + ... + k = k*(k+1)/2
Show: 1 + 2 + 3 + ... + k + (k + 1) = (k+1)*(k+2)/2
k*(k+1)/2 + (k+1) = k*(k+1)/2 + 2*(k+1)/2
Therefore, the statement "1 + 2 + 3 + ... + n = n*(n+1)/2" is true for all natural numbers n.
Here's a more complex example. Consider the Fibonacci Sequence, which goes {1,1,2,3,5,8,13,...}. Each number is the sum of the previous two numbers. Let's say that I've given you the following equation:
F(n) = nth Fibonacci number = (Φn - (-Φ)-n) / sqrt(5)
where Φ = 1/2 + sqrt(5)/2 This number is called the golden ratio.
How can you prove this equation is true for all natural numbers? First, you prove it for n=1 and n=2. Then, you show that if it's true for n = k and n = k+1, it must also be true for n = k+2.
But the actual proof might be too messy for a blog post ... so I leave it as an exercise to the reader (this is code for "I tried it, but I lost interest before finishing").
Anyways, the interesting thing about induction is that it only really helps you after you've found the equation for a sequence. Induction doesn't help in finding the equation itself. For example, if I hadn't given you the formula for the Fibonacci sequence, you would have nothing to work with. So how did I get that formula? The short answer is that I used mathematical intuition and a calculator.
So the moral that I'm tacking on here is that real math is not just the mindless execution of a bunch of instructions. Real math requires quite a bit of insight and intuition.
So let's say I wanted to prove the below equation for all natural numbers n. (The natural number are {1, 2, 3, 4, 5, ... }.)
1 + 2 + 3 + ... + n = n*(n+1)/2
First, let's test the equation for a few values of n.
1 = 1*(1+1)/2 = 1
1 + 2 = 2*(2+1)/2 = 3
1 + 2 + 3 = 3*(3+1)/2 = 6
1 + 2 + 3 + 4 = 4*(4+1)/2 = 10
So do you get the idea? But how do we prove that the equation is true for all n? There are infinite natural numbers, so we can't just go through them one by one.
What we use is a method called induction. First, we prove that the equation is true for n = 1. Second, we show that if it is true for n = k, it is also true for n = k+1. After we have proven this, we know that the equation is true for n = 1, and therefore n = 2, and therefore n = 3, and so on. The equation is true for n = {1, 2, 3, 4, 5, ...} = all natural numbers. It's that easy.
So here goes:
Step 1: 1 = 1*(1+1)/2 = 1
Step 2:
Assume: 1 + 2 + 3 + ... + k = k*(k+1)/2
Show: 1 + 2 + 3 + ... + k + (k + 1) = (k+1)*(k+2)/2
k*(k+1)/2 + (k+1) = k*(k+1)/2 + 2*(k+1)/2
Therefore, the statement "1 + 2 + 3 + ... + n = n*(n+1)/2" is true for all natural numbers n.
Here's a more complex example. Consider the Fibonacci Sequence, which goes {1,1,2,3,5,8,13,...}. Each number is the sum of the previous two numbers. Let's say that I've given you the following equation:
F(n) = nth Fibonacci number = (Φn - (-Φ)-n) / sqrt(5)
where Φ = 1/2 + sqrt(5)/2 This number is called the golden ratio.
How can you prove this equation is true for all natural numbers? First, you prove it for n=1 and n=2. Then, you show that if it's true for n = k and n = k+1, it must also be true for n = k+2.
But the actual proof might be too messy for a blog post ... so I leave it as an exercise to the reader (this is code for "I tried it, but I lost interest before finishing").
Anyways, the interesting thing about induction is that it only really helps you after you've found the equation for a sequence. Induction doesn't help in finding the equation itself. For example, if I hadn't given you the formula for the Fibonacci sequence, you would have nothing to work with. So how did I get that formula? The short answer is that I used mathematical intuition and a calculator.
So the moral that I'm tacking on here is that real math is not just the mindless execution of a bunch of instructions. Real math requires quite a bit of insight and intuition.
Wednesday, November 7, 2007
An odd experience
I just had the oddest experience. When I was asleep, suddenly my roommates started talking about science. They quickly moved through cosmology, onto metaphysics, and into philosophy and religion. It was rather surreal, and not just because I was half-asleep.
I guess I have this expectation whenever "normal" people talk that the subject will always be about daily life, entertainment, or sports (my mind edits out the last category for me). I guess it took me by surprise that anyone would start talking about other topics of their own accord. I was turning incredulously in my sleep.
Am I the only person who experiences a disconnect between the internet and real life?
I guess I have this expectation whenever "normal" people talk that the subject will always be about daily life, entertainment, or sports (my mind edits out the last category for me). I guess it took me by surprise that anyone would start talking about other topics of their own accord. I was turning incredulously in my sleep.
Am I the only person who experiences a disconnect between the internet and real life?
Tuesday, November 6, 2007
Special Relativity tangent: Time travel
Part 0: More historical background
Part 1: The problem
Part 2: Space-Time
Ok, I'm going to go off on another tangent, but I promise it will be interesting.
One thing that SR necessarily implies is that if you move faster than light, you can travel backwards in time. In the diagram below (see part 2 for an explanation of space-time diagrams), we are considering the yellow world line, which represents a particle moving at 3 times the speed of light.
 Note that the yellow particle is moving from the left side of the diagram to the right side. You might notice that I left one of the other world lines (dark blue) in there, along with its plane of simultaneity (light blue). This is to show that the yellow particle moves from after the plane of simultaneity to before the plane. Therefore, from the reference frame of the dark blue person, the yellow particle is moving backwards in time. This is true of anything that moves faster than light; there exists a reference frame in which that object is moving backwards in time.
Note that the yellow particle is moving from the left side of the diagram to the right side. You might notice that I left one of the other world lines (dark blue) in there, along with its plane of simultaneity (light blue). This is to show that the yellow particle moves from after the plane of simultaneity to before the plane. Therefore, from the reference frame of the dark blue person, the yellow particle is moving backwards in time. This is true of anything that moves faster than light; there exists a reference frame in which that object is moving backwards in time.
In advanced physics, sometimes you can come up with theories in which there are particles that always move faster than light. These particles are called tachyons. Despite being intriguing little things, tachyons are usually a sign that the theory needs improvement.
The problem with tachyons is that time travel creates numerous paradoxes. What if you go back in time and kill your grandfather? This is called the grandfather paradox. This can actually be a rather compelling argument against tachyons (unless they never interact). However, there are ways around this, as we can see in countless sci-fi stories. Perhaps history is quite resilient, and it is difficult to change anything so as to create paradoxes. Perhaps at the moment of a paradox, the entire universe disappears. Perhaps the entire universe splits into separate possibilities. Perhaps the rules of the universe just don't make any sense.
Although those are all great premises for a work of fiction, they're kind of far fetched as real physical theories if you ask me. But I think there's another way that Special Relativity allows for a sort of time travel. Under special relativity, you can make time go backwards just by accelerating! This is just a natural consequence of the tilting of the plane of simultaneity. Whenever you accelerate, your plane of simultaneity tilts in the direction of your motion. At a certain distance behind you, the plane of simultaneity is tilting faster than time is moving forward. Therefore, whenever you accelerate, any clocks more than a certain distance behind you move backwards.
I did the math, and this distance is equal to c2/a, where a is your acceleration, and c is the speed of light. That means that if you're in a car, and you accelerate from 0 to 60 mi/hr in 12 seconds facing directly away from alpha centauri (the nearest star aside from the sun), then all clocks on alpha centauri will start moving backwards (if I've done my math right). No paradoxes attached, since once you accelerate towards alpha centauri, the clocks will more than make up for their lost time.
That said, it will be impossible to actually observe the clocks moving backwards because of the manner in which the light would reach us.
Part 1: The problem
Part 2: Space-Time
Ok, I'm going to go off on another tangent, but I promise it will be interesting.
One thing that SR necessarily implies is that if you move faster than light, you can travel backwards in time. In the diagram below (see part 2 for an explanation of space-time diagrams), we are considering the yellow world line, which represents a particle moving at 3 times the speed of light.
 Note that the yellow particle is moving from the left side of the diagram to the right side. You might notice that I left one of the other world lines (dark blue) in there, along with its plane of simultaneity (light blue). This is to show that the yellow particle moves from after the plane of simultaneity to before the plane. Therefore, from the reference frame of the dark blue person, the yellow particle is moving backwards in time. This is true of anything that moves faster than light; there exists a reference frame in which that object is moving backwards in time.
Note that the yellow particle is moving from the left side of the diagram to the right side. You might notice that I left one of the other world lines (dark blue) in there, along with its plane of simultaneity (light blue). This is to show that the yellow particle moves from after the plane of simultaneity to before the plane. Therefore, from the reference frame of the dark blue person, the yellow particle is moving backwards in time. This is true of anything that moves faster than light; there exists a reference frame in which that object is moving backwards in time.In advanced physics, sometimes you can come up with theories in which there are particles that always move faster than light. These particles are called tachyons. Despite being intriguing little things, tachyons are usually a sign that the theory needs improvement.
The problem with tachyons is that time travel creates numerous paradoxes. What if you go back in time and kill your grandfather? This is called the grandfather paradox. This can actually be a rather compelling argument against tachyons (unless they never interact). However, there are ways around this, as we can see in countless sci-fi stories. Perhaps history is quite resilient, and it is difficult to change anything so as to create paradoxes. Perhaps at the moment of a paradox, the entire universe disappears. Perhaps the entire universe splits into separate possibilities. Perhaps the rules of the universe just don't make any sense.
Although those are all great premises for a work of fiction, they're kind of far fetched as real physical theories if you ask me. But I think there's another way that Special Relativity allows for a sort of time travel. Under special relativity, you can make time go backwards just by accelerating! This is just a natural consequence of the tilting of the plane of simultaneity. Whenever you accelerate, your plane of simultaneity tilts in the direction of your motion. At a certain distance behind you, the plane of simultaneity is tilting faster than time is moving forward. Therefore, whenever you accelerate, any clocks more than a certain distance behind you move backwards.
I did the math, and this distance is equal to c2/a, where a is your acceleration, and c is the speed of light. That means that if you're in a car, and you accelerate from 0 to 60 mi/hr in 12 seconds facing directly away from alpha centauri (the nearest star aside from the sun), then all clocks on alpha centauri will start moving backwards (if I've done my math right). No paradoxes attached, since once you accelerate towards alpha centauri, the clocks will more than make up for their lost time.
That said, it will be impossible to actually observe the clocks moving backwards because of the manner in which the light would reach us.
Monday, November 5, 2007
Random links
Everyone loves the internets.
- Greta Christina's Blog - Great blog with lots of cool thoughts and pictures. Recent case in point. Plus, she linked to me, so she obviously has good taste.
- Good Math Bad Math: Mathematical constructions - MarkCC discusses what axioms and definitions are. I sort of glossed over this in a previous post, but Mark actually knows what he's talking about whereas I don't.
- Infophilia: The Modus Tollens Exception - at some point I was planning on talking about when absence of evidence can be evidence of absence, but damn, Infophilia covered this several months ago, and I couldn't have said it better myself.
- a geocentric view: Turning a Sphere inside out - Topology video!
- Dresden Codak - Good news! Dresden Codak is now on a weekly update schedule. This webcomic brought us classics like this. "I have to find a way to get to school... WITH SCIENCE" I totally fantasize about saying something like that all the time.
Induction and the nature of fallacies
After I had read about induction and deduction in the Skeptic's Dictionary (my own take here), I started to recognize a pattern among some of the logical fallacies. The reason that some logical fallacies are compelling to some people is that they are actually inductive arguments. Inductive arguments, though they do not guarantee the conclusions, can be quite compelling under certain circumstances. Therefore, it stands to reason that there might be some cases where a fallacy is not a fallacy at all.
For a first example, take ad hominem and the related argument from authority. Oh yes, it's true that if crackpot makes an argument, our judgement on the crackpot ultimately has no bearing on our judgement of the argument itself. However, if there are time-constraints that prevent you from scrutinizing every single claim, would you not think it at least a little more likely that the biologists are right, and the guy who can't even understand entropy is wrong?
As a second example, take the fallacy of confusing correlation and causation. Yes, large feet are correlated with better spelling. Pirates are negatively correlated with global warming. But if atmospheric carbon dioxide levels are correlated with human output of carbon dioxide, you certainly can make a case that there is a causative link.
As a final example, consider the argument from ignorance. Just because I've never seen evidence for psychics doesn't mean that they don't exist. But, you know, I think that the absence of evidence, even after much searching, can in itself be rather compelling.
The point of this isn't at all to toss out the beloved baloney detection kit. Many fallacies may be inductive arguments, but they're called fallacies because the induction is nearly always very weak or completely invalid. Even the unusually good examples I showed above aren't nearly as powerful as other arguments I could have made for the same things. But experienced skeptics know that there are times when fallacies appear to apply when in fact they do not. So inquiring minds must know, what are the limits?
The limits are the same as those for induction. Induction is most powerful when it eliminates or weakens all competing claims. For the example with carbon dioxide, any competing claim would have to explain the apparent correlation. Yes, it can be done, but not as easily as with the claim of causation. For the psychics, my argument is not so compelling at first, since it is possible that I won't see any evidence whether psychics actually exist or not. However, if psychics did exist, we would expect that some well-designed experiments would provide evidence. So when experiments are performed, but no evidence is found, it is reasonable to argue that no psychics exist.
And of course, induction only reaches its full potential when combined with lots of other good evidence. In the carbon dioxide example, the argument would be greatly improved by a robust theory of the sources and sinks of atmospheric carbon dioxide. In the example with the biologists, the argument I provided is not very good just by itself, but may be supported by the fact that the guy not only misunderstands entropy, but also misunderstands biology, standard reasoning, and honesty. But for that argument to become truly compelling, there is no substitute for actually looking at the claims and debunking them.
So anyway, my entire point is that it is important to have a nuanced understand of fallacies, and not just apply them blindly as if they were infallible.
For a first example, take ad hominem and the related argument from authority. Oh yes, it's true that if crackpot makes an argument, our judgement on the crackpot ultimately has no bearing on our judgement of the argument itself. However, if there are time-constraints that prevent you from scrutinizing every single claim, would you not think it at least a little more likely that the biologists are right, and the guy who can't even understand entropy is wrong?
As a second example, take the fallacy of confusing correlation and causation. Yes, large feet are correlated with better spelling. Pirates are negatively correlated with global warming. But if atmospheric carbon dioxide levels are correlated with human output of carbon dioxide, you certainly can make a case that there is a causative link.
As a final example, consider the argument from ignorance. Just because I've never seen evidence for psychics doesn't mean that they don't exist. But, you know, I think that the absence of evidence, even after much searching, can in itself be rather compelling.
The point of this isn't at all to toss out the beloved baloney detection kit. Many fallacies may be inductive arguments, but they're called fallacies because the induction is nearly always very weak or completely invalid. Even the unusually good examples I showed above aren't nearly as powerful as other arguments I could have made for the same things. But experienced skeptics know that there are times when fallacies appear to apply when in fact they do not. So inquiring minds must know, what are the limits?
The limits are the same as those for induction. Induction is most powerful when it eliminates or weakens all competing claims. For the example with carbon dioxide, any competing claim would have to explain the apparent correlation. Yes, it can be done, but not as easily as with the claim of causation. For the psychics, my argument is not so compelling at first, since it is possible that I won't see any evidence whether psychics actually exist or not. However, if psychics did exist, we would expect that some well-designed experiments would provide evidence. So when experiments are performed, but no evidence is found, it is reasonable to argue that no psychics exist.
And of course, induction only reaches its full potential when combined with lots of other good evidence. In the carbon dioxide example, the argument would be greatly improved by a robust theory of the sources and sinks of atmospheric carbon dioxide. In the example with the biologists, the argument I provided is not very good just by itself, but may be supported by the fact that the guy not only misunderstands entropy, but also misunderstands biology, standard reasoning, and honesty. But for that argument to become truly compelling, there is no substitute for actually looking at the claims and debunking them.
So anyway, my entire point is that it is important to have a nuanced understand of fallacies, and not just apply them blindly as if they were infallible.
Categories:
fallacies,
reasoning,
skepticism
Sunday, November 4, 2007
The Monty Hall Problem
Difficulty: 3 of 10
Here's a puzzle that is truly a classic. It is based on an ancient game show with a host named Monty Hall.
In part of the show, a contestant chooses between three doors, only one of which has a fabulous prize. After choosing a single door, but before opening it, the game show host asks, "Would you change your mind if you saw this?" One of the other doors is opened, to reveal a goat (in case it isn't obvious, the goat is not the fabulous prize). Note that the game show host does this every single time, and always reveals a goat. The contestant is given the opportunity to either stick with the original decision or switch to the last unopened door.
So which would you choose? What is the probability of winning for each decision?
At first glance, it seems you have two equally likely choices, so you have a 1/2 chance of winning either way. But that just begs the question: are they in fact equally likely? Before any door is opened, you have a 1/3 probability of being correct. Does that probability suddenly jump up to 1/2 when a door is opened? No it doesn't. Therefore, you have a 2/3 probability of winning if you switch.
However, this puzzle has tripped up quite a number of extremely intelligent people, so allow me to argue the point. First consider three equally likely possibilities. Either you've picked goat 1, goat 2, or the fabulous prize. If you've picked goat 1, Monty Hall shows you goat 2. If you've picked goat 2, Monty Hall shows you goat 1. If you've picked the fabulous prize, Monty Hall has a 1/2 probability of showing you goat 1, and a 1/2 probability of picking goat 2. Here is a table of all the possibilities and their respective probabilities
Note that there are now four possibilities, but they are not equally likely. That is because the last two possibilities are merely the "splitting" of the last of the original three equally likely possibilities. For the first two possibilities, it would be better to switch. For the last two, it would be better to stay. So adding up the probabilities, you have a 2/3 chance of winning if you switch, and a 1/3 chance of winning if you stay.
So why is it that the door you picked stays at 1/3 probability, but the other door jumps from 1/3 to 2/3 as soon as a door is opened? It is because when Hall opens a door, you are given new information about the other two doors. Because Hall has zero chance of opening the door you picked, no new information is given about that door.
Here's a puzzle that is truly a classic. It is based on an ancient game show with a host named Monty Hall.
In part of the show, a contestant chooses between three doors, only one of which has a fabulous prize. After choosing a single door, but before opening it, the game show host asks, "Would you change your mind if you saw this?" One of the other doors is opened, to reveal a goat (in case it isn't obvious, the goat is not the fabulous prize). Note that the game show host does this every single time, and always reveals a goat. The contestant is given the opportunity to either stick with the original decision or switch to the last unopened door.
So which would you choose? What is the probability of winning for each decision?
At first glance, it seems you have two equally likely choices, so you have a 1/2 chance of winning either way. But that just begs the question: are they in fact equally likely? Before any door is opened, you have a 1/3 probability of being correct. Does that probability suddenly jump up to 1/2 when a door is opened? No it doesn't. Therefore, you have a 2/3 probability of winning if you switch.
However, this puzzle has tripped up quite a number of extremely intelligent people, so allow me to argue the point. First consider three equally likely possibilities. Either you've picked goat 1, goat 2, or the fabulous prize. If you've picked goat 1, Monty Hall shows you goat 2. If you've picked goat 2, Monty Hall shows you goat 1. If you've picked the fabulous prize, Monty Hall has a 1/2 probability of showing you goat 1, and a 1/2 probability of picking goat 2. Here is a table of all the possibilities and their respective probabilities
| 1/3 | You pick goat 1, Hall picks goat 2 |
| 1/3 | You pick goat 2, Hall picks goat 1 |
| 1/6 | You pick prize, Hall picks goat 1 |
| 1/6 | You pick prize, Hall picks goat 2 |
Note that there are now four possibilities, but they are not equally likely. That is because the last two possibilities are merely the "splitting" of the last of the original three equally likely possibilities. For the first two possibilities, it would be better to switch. For the last two, it would be better to stay. So adding up the probabilities, you have a 2/3 chance of winning if you switch, and a 1/3 chance of winning if you stay.
So why is it that the door you picked stays at 1/3 probability, but the other door jumps from 1/3 to 2/3 as soon as a door is opened? It is because when Hall opens a door, you are given new information about the other two doors. Because Hall has zero chance of opening the door you picked, no new information is given about that door.
Humanist Symposium #10

The Humanist Symposium #10 at Letters from a broad is up now. It includes my own short, humble submission. For those who don't know, the Humanist Symposium is a blogging carnival described here. It's all about the positive aspects of the atheist/humanist worldview, as opposed to criticisms of religion. Go read it!
For those who have come here through the carnival, welcome! And of course, I've got to insert the obligatory self-advertisement here (the real reason for this post?). On my blog, I like to talk about puzzles, science, skeptical reasoning, atheism, and other miscellaneous philosophizing. My blog's only a month old, so it's not too hard to browse the archives. Oh, and feedback is welcome, no, requested. Do I ramble? Are my topics uninteresting? Do I care too much what my readers think?
Saturday, November 3, 2007
Why do I care?
Though I seem to be intimately familiar with the contemporary skeptical and atheist movements, I never really considered myself an activist of any sort, though having an internet presence, however small, might put me in the running. I feel more like a spectator, or maybe a consumer of information. People like me probably constitute the majority of any sort of movement. I am the sort of guy who is all talk and no action. Oh, and have you heard of the "herding cats" problem? I'm part of that too!
All of this goes along with my background. I was an apathetic Catholic, and now I'm more of an apathetic atheist. I live in one of those backwards blue states, where everyone is friendly, tolerant, and open-minded. The predominant stereotype here is that atheists are much like people who are a little too interested in politics, only it's religion instead of politics. Around here, I can befriend a campus Christian group, and no one will care. I've never had any bad experiences with religious people. When asked why they care, atheists usually respond that, oh, religion is being stuffed down their throats, and they're sick of the nonsense. I have no such excuse, though of course I'm sensitive to the situations of other atheists throughout the country. So why should I care?
In a way, I don't, and I'm merely interested in the abstract reasoning put into the debate. Direct arguments against religion are unfashionable in some circles because it's preaching to the choir, convincing no one, and producing ill will. However, I think it's interesting from a pure reasoning and philosophical standpoint--it's fun to think, you know? And of course, I'm pathologically tactful about it, too.
But another reason to care is that it seems to me that atheism is one of the big trends of our time. We've all seen the polls. It's clear that the young generation--my generation--is becoming markedly less religious. The thought that I am a part of history is chilling. I don't know where it will lead, but I'd like to think that it will change things for the better. As part of this trend, I feel it is extremely important to know and understand it. Furthermore, I think it is important for everyone else, regardless of whether they think it's good or bad, to understand this movement. As a somewhat taboo topic, atheism is understood far less than it should be, resulting in a lack of sympathy from the public. The public must be informed--now that's something everyone can get behind.
So I think that is my purpose when I write. Alongside explanations of science and math, I also want to explain the movements that I am part of, what the people are like, and why I care.
All of this goes along with my background. I was an apathetic Catholic, and now I'm more of an apathetic atheist. I live in one of those backwards blue states, where everyone is friendly, tolerant, and open-minded. The predominant stereotype here is that atheists are much like people who are a little too interested in politics, only it's religion instead of politics. Around here, I can befriend a campus Christian group, and no one will care. I've never had any bad experiences with religious people. When asked why they care, atheists usually respond that, oh, religion is being stuffed down their throats, and they're sick of the nonsense. I have no such excuse, though of course I'm sensitive to the situations of other atheists throughout the country. So why should I care?
In a way, I don't, and I'm merely interested in the abstract reasoning put into the debate. Direct arguments against religion are unfashionable in some circles because it's preaching to the choir, convincing no one, and producing ill will. However, I think it's interesting from a pure reasoning and philosophical standpoint--it's fun to think, you know? And of course, I'm pathologically tactful about it, too.
But another reason to care is that it seems to me that atheism is one of the big trends of our time. We've all seen the polls. It's clear that the young generation--my generation--is becoming markedly less religious. The thought that I am a part of history is chilling. I don't know where it will lead, but I'd like to think that it will change things for the better. As part of this trend, I feel it is extremely important to know and understand it. Furthermore, I think it is important for everyone else, regardless of whether they think it's good or bad, to understand this movement. As a somewhat taboo topic, atheism is understood far less than it should be, resulting in a lack of sympathy from the public. The public must be informed--now that's something everyone can get behind.
So I think that is my purpose when I write. Alongside explanations of science and math, I also want to explain the movements that I am part of, what the people are like, and why I care.
Friday, November 2, 2007
The future of skepticism
Earlier, when a reader had sent me a news article about psychics, I privately thought to myself, "That seems like such old-fashioned skepticism." I'm not sure where I got this notion, but certain kinds of nonsense just strike me as pertaining more to the previous generation. This includes: psychics, clairvoyants, bigfoot, UFOs, ghosts, water dowsing, etc. Sure, some people still believe in these things, but they have largely fallen out of favor when compared to, say, the 70s. Skeptics feel like they're beating a dead horse; I feel like they're beating a dead horse.
On this note, I'd like to link to an an essay featured on Skepticality, the official podcast of the Skeptic's Society (also in pdf form). Skeptic Magazine editor Daniel Loxton talks about the goals and future of the skeptical movement. I found it both sad and inspiring, though people with a more normal sense of emotion might not feel the same way. I highly recommend listening to or reading it. (Thanks to Aardvarchaeology for the link.)
In brief, Daniel thinks that we should stick to the basic goals of skepticism, though the individual topics may change as different kinds of bunk go in and out of fashion. Of particular interest is that he thinks we should not link skepticism with libertarianism, humanism, or atheism. On this point, I agree. There may be noticeable overlaps, particularly with atheism, and there's no hiding that fact, but skepticism is a distinct concept from the others. I would hate to see anyone barred from skepticism just because they don't agree with a particular viewpoint that is common among the movement.
The essay also inspires me to debunk homeopathy in the future (however few readers I have). Daniel points out that this is one piece of bunk that has come into favor, despite being one of the most egregious examples of nonsense out there. Damn it, that makes even me angry.
On this note, I'd like to link to an an essay featured on Skepticality, the official podcast of the Skeptic's Society (also in pdf form). Skeptic Magazine editor Daniel Loxton talks about the goals and future of the skeptical movement. I found it both sad and inspiring, though people with a more normal sense of emotion might not feel the same way. I highly recommend listening to or reading it. (Thanks to Aardvarchaeology for the link.)
In brief, Daniel thinks that we should stick to the basic goals of skepticism, though the individual topics may change as different kinds of bunk go in and out of fashion. Of particular interest is that he thinks we should not link skepticism with libertarianism, humanism, or atheism. On this point, I agree. There may be noticeable overlaps, particularly with atheism, and there's no hiding that fact, but skepticism is a distinct concept from the others. I would hate to see anyone barred from skepticism just because they don't agree with a particular viewpoint that is common among the movement.
The essay also inspires me to debunk homeopathy in the future (however few readers I have). Daniel points out that this is one piece of bunk that has come into favor, despite being one of the most egregious examples of nonsense out there. Damn it, that makes even me angry.
Thursday, November 1, 2007
Special Relativity Part 2: Space-Time
This post will focus on the solution to the paradox in Part 1: The problem. Also see Part 0: More Historical Background. I should probably also cite this website, where I got the paradox. In fact, that website probably explains the resolution better than I, but I that hasn't stopped me before.
Before resolving this paradox, I think it is important to introduce the space-time diagram. (All diagrams were created by me in excel.)
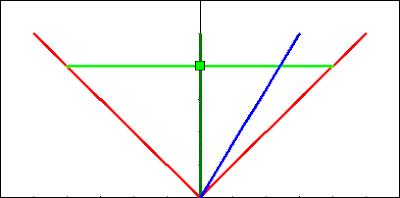 This is the diagram for the paradox I explained last time. The vertical axis represents time, and the horizontal axis represents space. The vertical dark-green line represents something that is staying still in space while moving through time--that represents me. This line is called my "world line" because it shows my path through space and time. The two red lines represent the world lines of two beams of light that I shoot forwards and backwards. Naturally, they move at the speed of light, which makes a 45 degree angle with the axes. The blue line represents you on your longboard, coasting forwards at 60% of the speed of light. At the initial point in time, you and I are in the same location. The light green line represents the "plane of simultaneity". All points on the plane of simultaneity happen at the same time.
This is the diagram for the paradox I explained last time. The vertical axis represents time, and the horizontal axis represents space. The vertical dark-green line represents something that is staying still in space while moving through time--that represents me. This line is called my "world line" because it shows my path through space and time. The two red lines represent the world lines of two beams of light that I shoot forwards and backwards. Naturally, they move at the speed of light, which makes a 45 degree angle with the axes. The blue line represents you on your longboard, coasting forwards at 60% of the speed of light. At the initial point in time, you and I are in the same location. The light green line represents the "plane of simultaneity". All points on the plane of simultaneity happen at the same time.
Of course, for our universe, which has three dimensions of space and one of time, a space-time diagram would actually have 4-dimensions. But that's too hard to draw, so I'm sticking to this. Another important note is that though everything on a plane of simultaneity really happens at the same time, it takes some time for the light to travel to my eyes before I see what's happening. Here, we do not talk about what I see, only what is.
In order to find if I am at the midpoint between the two beams of light, I first look to see where their world lines (red lines) intersect my plane of simultaneity (light green line). Then, I measure the distance between me (the green square) and the two intersections. The two distances are the same, so I must be at the midpoint.
But what of the paradox? How can you also be at the midpoint between the two beams of light? You're clearly closer to the one going forward than the one going backward. But once I draw your plane of simultaneity, all will become clear.
 The solution to all of this is that your plane of simultaneity is not parallel to mine. If you see two events happening at the same time, I would disagree and say they're happening at different times.
The solution to all of this is that your plane of simultaneity is not parallel to mine. If you see two events happening at the same time, I would disagree and say they're happening at different times.
In order see that you are at the midpoint of the two beams of light, you first find the intersections between your plane of simultaneity (light blue) and the world lines of the beams of light (red). Then you compare the distance between yourself (light blue square) and the two intersections. We really can be at two different midpoints!
From your point of view, of course, you'd be the one standing still, while the rest of the universe and I travel backwards. So the diagram below is from your point of view.
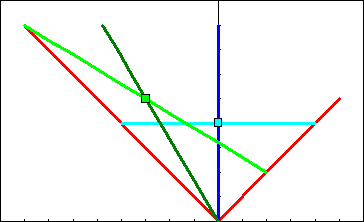 If you can imagine a smooth transition between this diagram to the previous one, you're in excellent shape. If you can't, maybe this animation will help.
If you can imagine a smooth transition between this diagram to the previous one, you're in excellent shape. If you can't, maybe this animation will help.
I drew these diagrams out so that the two squares, the green and blue ones, correspond to exactly one clock tick after the initial moment. Notice that from my point of view, my clock ticks before yours does. I must conclude that your clock is slower than mine. From your point of view, your clock ticks before mine does, so you must conclude that my clock is slower than yours. Yes, each clock is slower than the other, depending on your point of view. This effect is called "time dilation", and it becomes greater at greater speeds.
Notice that the light green and light blue lines change length depending on your point of view. This is because of an effect called "Lorentz contraction". From your point of view, all distances would appear shorter than usual. I would appear to be skinnier than usual. From my point of view, you would appear to be skinnier than usual. This effect becomes greater at greater speeds.
But before you start concocting relativistic schemes to become skinnier, I'll add that you also become heavier than usual. The reasons why are to be explained in Part 3.
I will take questions.
Before resolving this paradox, I think it is important to introduce the space-time diagram. (All diagrams were created by me in excel.)
 This is the diagram for the paradox I explained last time. The vertical axis represents time, and the horizontal axis represents space. The vertical dark-green line represents something that is staying still in space while moving through time--that represents me. This line is called my "world line" because it shows my path through space and time. The two red lines represent the world lines of two beams of light that I shoot forwards and backwards. Naturally, they move at the speed of light, which makes a 45 degree angle with the axes. The blue line represents you on your longboard, coasting forwards at 60% of the speed of light. At the initial point in time, you and I are in the same location. The light green line represents the "plane of simultaneity". All points on the plane of simultaneity happen at the same time.
This is the diagram for the paradox I explained last time. The vertical axis represents time, and the horizontal axis represents space. The vertical dark-green line represents something that is staying still in space while moving through time--that represents me. This line is called my "world line" because it shows my path through space and time. The two red lines represent the world lines of two beams of light that I shoot forwards and backwards. Naturally, they move at the speed of light, which makes a 45 degree angle with the axes. The blue line represents you on your longboard, coasting forwards at 60% of the speed of light. At the initial point in time, you and I are in the same location. The light green line represents the "plane of simultaneity". All points on the plane of simultaneity happen at the same time.Of course, for our universe, which has three dimensions of space and one of time, a space-time diagram would actually have 4-dimensions. But that's too hard to draw, so I'm sticking to this. Another important note is that though everything on a plane of simultaneity really happens at the same time, it takes some time for the light to travel to my eyes before I see what's happening. Here, we do not talk about what I see, only what is.
In order to find if I am at the midpoint between the two beams of light, I first look to see where their world lines (red lines) intersect my plane of simultaneity (light green line). Then, I measure the distance between me (the green square) and the two intersections. The two distances are the same, so I must be at the midpoint.
But what of the paradox? How can you also be at the midpoint between the two beams of light? You're clearly closer to the one going forward than the one going backward. But once I draw your plane of simultaneity, all will become clear.
 The solution to all of this is that your plane of simultaneity is not parallel to mine. If you see two events happening at the same time, I would disagree and say they're happening at different times.
The solution to all of this is that your plane of simultaneity is not parallel to mine. If you see two events happening at the same time, I would disagree and say they're happening at different times.In order see that you are at the midpoint of the two beams of light, you first find the intersections between your plane of simultaneity (light blue) and the world lines of the beams of light (red). Then you compare the distance between yourself (light blue square) and the two intersections. We really can be at two different midpoints!
From your point of view, of course, you'd be the one standing still, while the rest of the universe and I travel backwards. So the diagram below is from your point of view.
 If you can imagine a smooth transition between this diagram to the previous one, you're in excellent shape. If you can't, maybe this animation will help.
If you can imagine a smooth transition between this diagram to the previous one, you're in excellent shape. If you can't, maybe this animation will help.I drew these diagrams out so that the two squares, the green and blue ones, correspond to exactly one clock tick after the initial moment. Notice that from my point of view, my clock ticks before yours does. I must conclude that your clock is slower than mine. From your point of view, your clock ticks before mine does, so you must conclude that my clock is slower than yours. Yes, each clock is slower than the other, depending on your point of view. This effect is called "time dilation", and it becomes greater at greater speeds.
Notice that the light green and light blue lines change length depending on your point of view. This is because of an effect called "Lorentz contraction". From your point of view, all distances would appear shorter than usual. I would appear to be skinnier than usual. From my point of view, you would appear to be skinnier than usual. This effect becomes greater at greater speeds.
But before you start concocting relativistic schemes to become skinnier, I'll add that you also become heavier than usual. The reasons why are to be explained in Part 3.
I will take questions.
Subscribe to:
Comments (Atom)








