Special Relativity Part 2: Space-Time

This post will focus on the solution to the paradox in Part 1: The problem. Also see Part 0: More Historical Background. I should probably also cite this website, where I got the paradox. In fact, that website probably explains the resolution better than I, but I that hasn't stopped me before.

Before resolving this paradox, I think it is important to introduce the space-time diagram. (All diagrams were created by me in excel.)

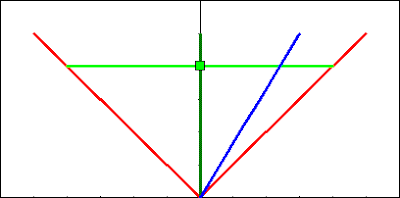This is the diagram for the paradox I explained last time. The vertical axis represents time, and the horizontal axis represents space. The vertical dark-green line represents something that is staying still in space while moving through time--that represents me. This line is called my "world line" because it shows my path through space and time. The two red lines represent the world lines of two beams of light that I shoot forwards and backwards. Naturally, they move at the speed of light, which makes a 45 degree angle with the axes. The blue line represents you on your longboard, coasting forwards at 60% of the speed of light. At the initial point in time, you and I are in the same location. The light green line represents the "plane of simultaneity". All points on the plane of simultaneity happen at the same time.

Of course, for our universe, which has three dimensions of space and one of time, a space-time diagram would actually have 4-dimensions. But that's too hard to draw, so I'm sticking to this. Another important note is that though everything on a plane of simultaneity really happens at the same time, it takes some time for the light to travel to my eyes before I see what's happening. Here, we do not talk about what I see, only what is.

In order to find if I am at the midpoint between the two beams of light, I first look to see where their world lines (red lines) intersect my plane of simultaneity (light green line). Then, I measure the distance between me (the green square) and the two intersections. The two distances are the same, so I must be at the midpoint.

But what of the paradox? How can you also be at the midpoint between the two beams of light? You're clearly closer to the one going forward than the one going backward. But once I draw your plane of simultaneity, all will become clear.

The solution to all of this is that your plane of simultaneity is not parallel to mine. If you see two events happening at the same time, I would disagree and say they're happening at different times.

In order see that you are at the midpoint of the two beams of light, you first find the intersections between your plane of simultaneity (light blue) and the world lines of the beams of light (red). Then you compare the distance between yourself (light blue square) and the two intersections. We really can be at two different midpoints!

From your point of view, of course, you'd be the one standing still, while the rest of the universe and I travel backwards. So the diagram below is from your point of view.
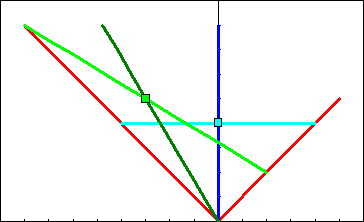If you can imagine a smooth transition between this diagram to the previous one, you're in excellent shape. If you can't, maybe this animation will help.

I drew these diagrams out so that the two squares, the green and blue ones, correspond to exactly one clock tick after the initial moment. Notice that from my point of view, my clock ticks before yours does. I must conclude that your clock is slower than mine. From your point of view, your clock ticks before mine does, so you must conclude that my clock is slower than yours. Yes, each clock is slower than the other, depending on your point of view. This effect is called "time dilation", and it becomes greater at greater speeds.

Notice that the light green and light blue lines change length depending on your point of view. This is because of an effect called "Lorentz contraction". From your point of view, all distances would appear shorter than usual. I would appear to be skinnier than usual. From my point of view, you would appear to be skinnier than usual. This effect becomes greater at greater speeds.

But before you start concocting relativistic schemes to become skinnier, I'll add that you also become heavier than usual. The reasons why are to be explained in Part 3.

I will take questions.