Entanglement explained

Most popular explanations of quantum entanglement will describe it as a mysterious connection between particles. It's "spooky action at a distance", to quote Einstein. However, it is my firm opinion that mysteriousness and spookiness should not be excuses to stop explaining things. It should not surprise you to know that physicists understand quantum entanglement a lot better than they let on. It's just that it's rather mathematically involved, and therefore difficult to explain to popular audiences. Lucky for you, I enjoy attempting such futile tasks.

Let us build entanglement from the ground up, starting with wavefunctions. Here is an example of a wavefunction:

The wavefunction is just some abstract mathematical object which can be used to describe the particle. If you square the wavefunction, like this...
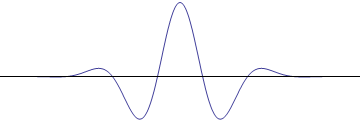
...then you get the probability of finding the particle at different locations. The particle is most likely to be found in that big hump in the middle, but there's also a chance that it will be found on either of the humps on the left or the right. There's also a very small chance that it will be found much further away from the center.

Another thing you can tell by looking at the wavefunction is the particle's momentum (mass times velocity). The momentum of the particle is related to how wavy the wavefunction is. For instance, if the wavefunction looked like this...
...then the particle will have a much higher momentum than in the first wavefunction. If you try to measure the particle's velocity, it will probably be moving very quickly either to the right or to the left.

But particles don't just move to the right and left. They can go right, left, forward, backwards, up, and down. We live in a three-dimensional world. The above wavefunctions only show one of those dimensions. Here is an example of a two-dimensional wavefunction:

What does this wavefunction tell you? If you try to measure the Y position of the particle, it will appear near the center. However, the X position of the particle is a bit more uncertain. It will either appear to the right, in the valley, or to the left, on the hill.

But "left" and "right" are relative. If we just turn around 180 degrees, left becomes right, and right becomes left. If we turn around 90 degrees, the X and Y coordinates switch places. And if we turn 45 degrees...

...we get this.

Let's say we tried to measure the Y position of the particle, and got something to the left of center, right where that big hill is. Then we already know that the X position will probably be to the left of center too, before we directly measure it. And if we found that the Y position was to the right of center, we could predict that the X position would also be to the right of center. The X and Y coordinates of the particle are correlated. I might even say that the X and Y coordinates have a "mysterious connection" between them.

What makes this mysterious correlation so special? Why do we need to say that the particle is in both places at once? Couldn't we just say that we don't know its precise location? Couldn't we just say that there's a chance that both X and Y are right of center, and a chance that they're both left of center? The answer is no. The particle is in both locations at once, until we measure it. Recall that the momentum of the particle is described by the waviness of the wavefunction. If the particle were only in one of the two locations, that would affect its waviness, so to speak, thus affecting its momentum.

That's the basic idea of how we add new dimensions to quantum mechanics. We take what's called the Cartesian product of the X axis and the Y axis, and we get the X-Y plane. We can take another Cartesian product with the Z axis to make it three dimensional.

When we look at a quantum mechanical system with two particles, it is not described with two separate wavefunctions. There is always only one wavefunction. Instead, we take the Cartesian Product of the two particles' positions, like so.

Notice that the positions of the two particles are now mysteriously correlated. This may occur even if the particles are very far away from each other. By measuring one particle, we instantly get information about the other particle, even if it's light-years away. But before we take any measurements, both particles are in both locations.

Of course, each particle really requires not one, but three dimensions to describe its position. So for two particles, we really need six dimensions to describe them both. If we have three particles, we need a 9-dimensional space. If we have thousand particles, we need a 3000-dimensional space. In principle, the entire universe would be described with a single wavefunction with an absurdly huge number of dimensions.

And that's not even including non-spatial dimensions, which also have to be multiplied in. Non-spatial dimensions include spin and polarization. In fact, most popular explanations of quantum entanglement start out with correlations of polarization between two photons. It's the same idea, really. The main difference is that there are only two polarizations (horizontal and vertical), but there are an infinite number of positions (ie 1, 1/100, pi, 42). That makes it much easier to analyze and study under controlled conditions.

Let's take a step back and see what happened here. If we have a multi-dimensional wavefunction, the different dimensions can be correlated with each other. Adding new particles is just a matter of adding new dimensions to the wavefunction. Therefore, separate particles, too, can be correlated with each other. These correlations can extend across large distances. Measuring a particle here can instantly and indirectly measure a particle on the other side of the galaxy. It's almost, but not quite, as if you received a message from the other side of the galaxy at a speed far faster than light. The consequences of entanglement, even I'll admit, are quite profound and mysterious. But where entanglement came from is not mysterious. It was just quietly encoded in the math all along.