I want to have a little discussion about causation. And to get your attention, I will start with an outlandish statement.
Being female causes a person to not study physics.
It sounds outrageous, but it isn't when you examine the meaning closely. The only thing outrageous here is my cheap attention-grabbing tactic.
What does it mean for something to cause something else? It's difficult to explain, because it's sort of an intuitive concept. A good place to start is by looking at the definition of causation in science.
In science, a causal relationship is proven by varying the cause, and measuring a difference in the effect. For example, suppose that we're considering the idea that eating vegetables causes you to grow taller (silly example, I know, but just go with it). The way to test this is by take a group of people and feeding them different amounts of vegetables. Then we measure the change in their height.
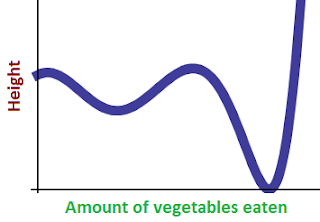
If the results looks like this, then we may have a causal relationship!
Of course, I'm ignoring a few things like randomness. Clearly some people grow taller than others, regardless of diets. That doesn't mean that there is no causal relationship, it just means that you'll have to do some averaging or other statistical analysis first. Eventually, you should get a straight line like above, and then you've found evidence for causation.
Note that you can have different degrees of causation. If you have a very steep line, that means that vegetables cause you to grow a lot taller. If it's a shallow line, vegetables just cause you to grow a little taller. But we may also get a wonky mix of shallow and steep slopes, and even negative slopes.
There is some sort of causal relationship here, but the slope of the line changes so much that we can't even say if more vegetables will make you taller or shorter. It seems to depend on how much vegetables you were eating to begin with. This isn't an unusual scenario; many causal relationships turn out to be nonlinear if you consider a wide enough range. Perhaps the language of causation is not sufficient to describe the situation.
There's another important component I missed. Imagine that I decided to put all the teenagers into the group fed with lots of vegetables, and put all the older subjects into the group with fewer vegetables. This would compromise my evidence since teenagers grow a lot faster than adults.
The thing to understand is that there are a lot more variables than just the amount of vegetables eaten. The way to test the effect of vegetables is to vary the amount of vegetables while holding other variables constant, such as age. Or, since every person is different, you could just randomly assign them to groups. When the groups are randomized, the averages are roughly constant. For instance, two randomized groups will probably have about the same average age.
But this introduces new kinds of trickiness. For instance, if we are testing the effect of eating vegetables, which variables are we holding constant? Are we holding the amount of non-vegetables constant? Are we holding constant the total amount eaten? Or are we holding constant something else entirely?
The above plot represents a possible relationship between the amount of vegetables eaten, the amount of non-vegetables eaten, and the change in height. The blue line represents what we find if we hold constant the amount of non-vegetables eaten. The green line represents what we find if we hold constant the total amount eaten. If we look at the blue line, vegetables make you taller. If we look at the green line, vegetables make you shorter. Which is it?
Yet again, I will suggest that the language of causation is not enough to describe the situation. It's not enough to say that vegetables cause this, or cause that, without saying which variables are held constant.
Let's go back to the statement about females. When everyone is born, they're assigned more or less randomly either male or female. Because it's random, all other variables determined at birth are roughly constant. And then I make the observation that fewer women study physics than men. Therefore, being female causes a person to not study physics. I've proven it by a natural ongoing experiment.
But note that I only held constant the variables which are determined at birth. What if I also decided to hold constant another variable: society's treatment of the person? That is, both the female and male groups must be treated the same by everyone. What's the causal relationship, if any? Unfortunately, this experiment is too difficult to carry out.
Other posts in this mini-series:
Colds and Causality
Women and Causality
Responsibility and Causality
Nature/nurture and Causality
Physics and Causality
Math and Causality
Tuesday, July 27, 2010
Subscribe to:
Post Comments (Atom)











0 comments:
Post a Comment