To briefly summarize I&J, they formulate the FTA in bayesian terms. We already know that life exists, as part of our background knowledge. The new piece of evidence put forth by the FTA is that the universe is such that life may arise naturalistically (ie it is "life-friendly"). I&J say the problem is that this evidence argues against supernaturalism, not in favor of it. After all, in a naturalistic world, we must observe that the universe is life-friendly. In a supernaturalistic world, we might observe otherwise, since supernatural intervention can create or sustain life even when natural laws are not life-friendly.
In formal terms:2
N = universe is naturalisticI think their theorem is basically incontrovertible,3 and I do not contest it. However, I feel it is missing the point. Here I aim to explain why.
L = life exists
F = universe is life-friendly
I&J show that
P(N|F&L) ≥ P(N|L)
Whereas the FTA requires that
P(N|F&L) << P(N|L)
What does the Fine-Tuning argument argue?
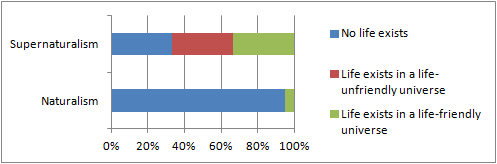
A schematic illustration of the Fine-Tuning argument. The two rows each represent a different meta-theory of the universe. The colored bars represent the probabilities of different events within those meta-theories.
The FTA asks us to compare two meta-theories of the universe: naturalism and supernaturalism. In a naturalistic universe, there's a very small probability that life can arise, because the universal constants need to be just right (or so the argument goes). In a supernatural universe, well, who knows?
I&J make two important points about this argument. First, they argue that the premise is irrelevant, and the conclusion is a fallacy. Formally:
Premise: P(F|N) << 1I checked to see if this is in fact the premise and conclusion used by FTA proponents. The Discovery Institute basically makes the following argument:
Fallacious conclusion: P(N|F) << 1
Premise: P(F|N) < P(F|~N)This is similar to the fallacious reasoning identified by I&J, only it's not fallacious. It's correct. But it requires a stronger premise. Namely, we have to assume that the probability of life under naturalism is less than the probability of life under supernaturalism (as illustrated above).
Conclusion: P(N|F) < P(N)
I believe that I&J reject this stronger premise, and I think this is reasonable. Who is to say that a deity would be particularly likely to arrange the universe such that it contains life? There are an infinite number of possible deities which each prefer a different configuration of the universe. If we only speak of deities that have an inclination towards universes with life, then they're likely to create life, but this is just some sort of selection bias on our part.
But even though I tentatively agree with I&J's first point, I will ignore it for the rest of the post, because I wish to evaluate how their second point stands on its own.
I&J's second point is that we need to include all evidence in our Bayesian. We know two things: life exists, and life can arise. The probability of naturalism should be conditioned on both these facts, not just one or the other. Formally:
FTA argues that P(N|F) > P(N)
But the relevant comparison is between the quantitities P(N|F&L) and P(N|L)
On the other hand, if we compare the size of the green bars, it seems like the FTA works. If the universe is life-friendly, that is evidence for naturalism. But if the universe has life in it, it seems like that's even stronger evidence for the supernatural. In formal terms, it appears that
P(N|F&L) ≥ P(N|L) << P(N)And that's why I feel I&J have missed the point.
Life-friendliness vs Life
The "fine tuning" argument isn't "What do you think about God, when you learn that you are alive?" but "What do you think about God, when you learn that the universe is (apparently) fine-tuned or life-friendly?"As in the quote above, I&J believe that the only piece of evidence advanced by the FTA is that the universe is life-friendly. The existence of life is not a piece of evidence, because we already knew life existed.
--Ikeda & Jefferys
The thing is, the distinction between "life exists" and "life can arise naturalistically" is a novel idea by I&J. It is definitely a useful distinction that improves our understanding of the problem. But I don't think FTA proponents ever make this distinction. FTA proponents are vague about it, and may not even know themselves whether they are arguing about life-friendliness or life-existence.
Therefore, when I&J say that FTA proponents are using life-friendliness as evidence, and not life-existence, this is totally groundless.
To understand the distinction between life-friendliness and the existence of life, it may help to consider how we might demonstrate life-friendliness. It's actually very difficult to demonstrate without any sort of presumption of naturalism. I&J indirectly mention the triple-alpha process, wherein the helium inside of stars fuse to carbon. Since the triple-alpha process is necessary to naturalistically produce carbon life-forms, Fred Hoyle predicted in the 1950s that there was a particular resonance which greatly increased the probability of the triple-alpha process. This prediction was later confirmed.
If FTA proponents are truly using life-friendliness as their evidence, they would point to Fred Hoyle's confirmed prediction. In Biologos treatment, they do discuss the triple-alpha process, but do not mention Hoyle's confirmed prediction. Instead they talk about how "statistically unusual" the resonance is.
Put in formal terms, I&J say that we should compare the quantities P(N|F&L) and P(N|L), because this is the correct comparison, and because this is the comparison described by FTA proponents themselves. But I think that FTA proponents are actually comparing P(N|F&L) and P(N). Furthermore, I think FTA proponents have chosen the correct comparison, whereas I&J have chosen the wrong one.
Trickiness with priors
But what is P(N|L)/P(~N|L)? Why, it is just the prior odds ratio that You assign to describe Your relative belief in N and ~N before You learn that F is true.According to I&J, our prior beliefs are based on our knowledge that life exists. We think, therefore we are. Therefore, if upon seeing that life exists, you think that supernaturalism is more likely than naturalism, then you have a "prior commitment" to supernaturalism.
--Ikeda & Jefferys
"Prior commitment" sounds bad, like you've decided your conclusions before you've considered the evidence. But generally speaking, there's nothing wrong with coming to conclusions without evidence, if you have an a priori argument. Since FTA proponents are arguing about the quantity P(N|L), which I&J call a prior probability, we could say that FTA is partly an a priori argument.
Is it really true that the FTA is an a priori argument? If the only evidence advanced is the existence of life, then the FTA is quite similar to the cosmological argument. The cosmological argument only advances the evidence that there exists something rather than nothing. Is the cosmological argument considered an a priori argument? The internet consensus seems to be not.4
If the FTA is not an a priori argument, then I&J have made an error in using P(N|L) as our prior belief, rather than P(N). If the FTA is an a priori argument, then I&J have basically ignored the a priori component of it, and no wonder that what remains is so unconvincing.
Of course, it seems like FTA proponents really are trying to advance some sort of evidence, and that's why they talk about universal constants and the triple-alpha process. I propose that what's happening is that we're actually comparing three meta-theories:
By eliminating the naturalistic theories where fine-tuning is not necessary, it seems we greatly reduce the probability of life existing within naturalism.
Conclusion (TL;DR)
Ikeda and Jefferys refute the Fine-Tuning argument by making an interesting and useful distinction between universes with life, and universes where life can arise naturally. According to them, it is only necessary to consider the evidence that life can arise naturally. The problem is that this ignores the main thrust of the Fine-Tuning argument.
To refute the Fine-Tuning argument, we must discuss its many other problems, and not the particular problem put forth by Ikeda and Jefferys.
--------------------------------------------
1. Also see the same paper hosted on a different website with inferior design, but with the extra Appendix 2.
2. If you are unfamiliar with the formalism of conditional probabilities, you can read up on it. In this post, I will try to minimize formalism, but it is impossible to eliminate it entirely.
3. The only assumption is that P(~F&L&N) = 0, which is true from the definition of F.
4. See here, here, and here, all search results for the cosmological argument.
