I just got back from March Meeting, the one of the world's largest physics conferences. I thought I'd share one talk which used relatively basic physics to explain a surprising phenomenon:
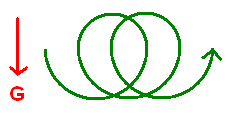
Summary for people who don't watch videos: You have a long chain of metal beads in a beaker, and you let the chain fall out. Rather than slithering over the edge of the beaker, the chain jumps out of the beaker. It turns out the explanation has to do with the shape of the beads; when the chain is pulled out, geometry requires that the beaker gives the beads an extra kick.
I think it could be a neat science fair experiment for someone to design a chain which produces a larger fountain. The chain needs to be made of long beads, whose mass is concentrated in the middle. I'm not sure what you would make the beads out of.
Showing posts with label mechanics. Show all posts
Showing posts with label mechanics. Show all posts
Saturday, March 7, 2015
Monday, June 4, 2012
Irrational physics
In physics, you expect that it doesn't really matter whether a number is rational or irrational. Physics measurements rarely have perfect precision. If you measure a number to be 0.750000, it sure looks like the rational number 3/4, but it may be just slightly different, after the sixteenth decimal place. Who can say?
But rational and irrational numbers sometimes make a difference.
Consider the case of two crystals. On the atomic level, the surfaces of these crystals are very bumpy. You would expect that when you place one crystal on top of the other, the bumps on the top crystal's surface would prefer to align with the grooves on the bottom crystal's surface. But what if the bumps on the top crystal and the bumps on the bottom crystal are spaced differently? Will one crystal squeeze or stretch to fit the other? Or will the crystals just lay on top of each other, bumps and grooves be damned?
As usual, we solve this problem by considering a simpler problem: a string of atoms sitting on top of a bumpy surface. The atoms behave like they are attached by springs. There is a preferred distance between two atoms, which we'll call distance A. You can push the atoms closer to each other by compressing the springs, or pull them apart by stretching the springs, but it requires energy to do so. It also requires energy to place an atom on a bump rather than a groove. The bumps are evenly spaced, with distance B between each bump.
At low temperature, the atoms will settle down to the lowest energy state. But the lowest energy state depends on the ratio A/B. Specifically, it depends on whether A/B is "nearly rational", or if it is "sufficiently irrational".
So let us first consider the case where A/B is nearly rational. For simplicity's sake, let's say A/B is near the rational number 1. Of course, if A/B is exactly one, then the atoms will all slide to the lowest points of the bumpy surface, and that's that. But if A/B is just a little different, then the atoms will still lie at the lowest points of the bumpy surface. It may cost a little bit of energy to stretch or compress the springs a little, but it would cost even more energy to have the atoms completely unaligned with the bumpy surface.
On the other hand, if A/B is too far from 1, then the energy cost of stretching or compressing the springs just to get all the atoms exactly at the grooves is too much. It requires less energy to just have the atoms evenly spaced, even if that means that they're scattered all over the groove structure from high to low.
The former scenario is called the commensurate phase. The latter scenario is called the incommensurate phase. You can imagine the ratio A/B changing (perhaps the bumps shrink as the temperature changes), leading to a phase transition between commensurate and incommensurate. Yes, just like the phase transition between solid, liquid, and gas. In condensed matter we talk about all sorts of subtle phases, and the phase transitions between them.
As for where exactly the phase transition occurs, you have to know something about the strength of the springs, the height and shape of the bumps, and which rational number is being considered. Bigger bumps means that the system is commensurate for a larger range of values of A/B. Typically,* the larger the denominator of the rational number, the smaller the commensurate range. So you can imagine that there is a large commensurate range around 1, a smaller range around 1/2, and an even smaller range around 7/9.
*This depends on the exact shape of the bumps. If the bumps are perfect sine waves, I believe most rational numbers don't produce any commensurate phase whatsoever.
But even though the rational numbers are densely packed on the number line, the commensurate phase does not necessarily cover all numbers. That may be hard for the non-mathematicians to grok, but imagine that the commensurate ranges get exponentially smaller as you include more and more rational numbers. If you sum up all the terms in an exponentially decreasing series (eg 1/2 + 1/4 + 1/8 + 1/16 + ...), you get a finite number. It could be the case that this number is less than the total length of the numbers we're considering. If that is the case, there must be some numbers which are not covered by any of the commensurate phases.
We call these numbers "sufficiently irrational." If A/B is sufficiently irrational, then the incommensurate phase is stable.
Of course, this only applies at absolute zero temperature, when there is an infinite string of atoms. In a real system, here's no need to consider rational numbers with denominators greater than the number of atoms. On the other hand, in a real system, there are about 10^8 atoms in a centimeter. On the other other hand, a nonzero temperature will kill a lot of commensurate phases, since the random motion of atoms would be enough to overcome the tiny amount of energy saved by being in the commensurate phase.
The complications of reality notwithstanding, I think it is mathematically beautiful to think of all these commensurate phases arranged in a fractal pattern.
This fractal pattern also appears somewhere else in physics--chaos theory. If the initial conditions of a system are nearly rational, the system may follow a completely different trajectory than if the initial conditions were sufficiently irrational. Since it's hard for us to know, with our imperfect measurements, whether a number is sufficiently irrational or not, the system may be unpredictable. That's what leads to chaotic motion.
But rational and irrational numbers sometimes make a difference.
Consider the case of two crystals. On the atomic level, the surfaces of these crystals are very bumpy. You would expect that when you place one crystal on top of the other, the bumps on the top crystal's surface would prefer to align with the grooves on the bottom crystal's surface. But what if the bumps on the top crystal and the bumps on the bottom crystal are spaced differently? Will one crystal squeeze or stretch to fit the other? Or will the crystals just lay on top of each other, bumps and grooves be damned?
As usual, we solve this problem by considering a simpler problem: a string of atoms sitting on top of a bumpy surface. The atoms behave like they are attached by springs. There is a preferred distance between two atoms, which we'll call distance A. You can push the atoms closer to each other by compressing the springs, or pull them apart by stretching the springs, but it requires energy to do so. It also requires energy to place an atom on a bump rather than a groove. The bumps are evenly spaced, with distance B between each bump.
At low temperature, the atoms will settle down to the lowest energy state. But the lowest energy state depends on the ratio A/B. Specifically, it depends on whether A/B is "nearly rational", or if it is "sufficiently irrational".
So let us first consider the case where A/B is nearly rational. For simplicity's sake, let's say A/B is near the rational number 1. Of course, if A/B is exactly one, then the atoms will all slide to the lowest points of the bumpy surface, and that's that. But if A/B is just a little different, then the atoms will still lie at the lowest points of the bumpy surface. It may cost a little bit of energy to stretch or compress the springs a little, but it would cost even more energy to have the atoms completely unaligned with the bumpy surface.
On the other hand, if A/B is too far from 1, then the energy cost of stretching or compressing the springs just to get all the atoms exactly at the grooves is too much. It requires less energy to just have the atoms evenly spaced, even if that means that they're scattered all over the groove structure from high to low.
The former scenario is called the commensurate phase. The latter scenario is called the incommensurate phase. You can imagine the ratio A/B changing (perhaps the bumps shrink as the temperature changes), leading to a phase transition between commensurate and incommensurate. Yes, just like the phase transition between solid, liquid, and gas. In condensed matter we talk about all sorts of subtle phases, and the phase transitions between them.
As for where exactly the phase transition occurs, you have to know something about the strength of the springs, the height and shape of the bumps, and which rational number is being considered. Bigger bumps means that the system is commensurate for a larger range of values of A/B. Typically,* the larger the denominator of the rational number, the smaller the commensurate range. So you can imagine that there is a large commensurate range around 1, a smaller range around 1/2, and an even smaller range around 7/9.
*This depends on the exact shape of the bumps. If the bumps are perfect sine waves, I believe most rational numbers don't produce any commensurate phase whatsoever.
But even though the rational numbers are densely packed on the number line, the commensurate phase does not necessarily cover all numbers. That may be hard for the non-mathematicians to grok, but imagine that the commensurate ranges get exponentially smaller as you include more and more rational numbers. If you sum up all the terms in an exponentially decreasing series (eg 1/2 + 1/4 + 1/8 + 1/16 + ...), you get a finite number. It could be the case that this number is less than the total length of the numbers we're considering. If that is the case, there must be some numbers which are not covered by any of the commensurate phases.
We call these numbers "sufficiently irrational." If A/B is sufficiently irrational, then the incommensurate phase is stable.
Of course, this only applies at absolute zero temperature, when there is an infinite string of atoms. In a real system, here's no need to consider rational numbers with denominators greater than the number of atoms. On the other hand, in a real system, there are about 10^8 atoms in a centimeter. On the other other hand, a nonzero temperature will kill a lot of commensurate phases, since the random motion of atoms would be enough to overcome the tiny amount of energy saved by being in the commensurate phase.
The complications of reality notwithstanding, I think it is mathematically beautiful to think of all these commensurate phases arranged in a fractal pattern.
This fractal pattern also appears somewhere else in physics--chaos theory. If the initial conditions of a system are nearly rational, the system may follow a completely different trajectory than if the initial conditions were sufficiently irrational. Since it's hard for us to know, with our imperfect measurements, whether a number is sufficiently irrational or not, the system may be unpredictable. That's what leads to chaotic motion.
Friday, April 10, 2009
Forks and Torques
Today is a good day I think to rationalize trivial personal quirks.
For example, I have the quirk that I hold forks and spoons in an improper way.
If you're holding a spoon or a fork alone, you're supposed to hold it with your thumb and index finger as it rests on the side of your middle finger. This really needs a picture, but unfortunately, the only one I could find is copyrighted, and I don't feel comfortable taking it. Hopefully, the lack of pictures on the net means that most people simply don't care about etiquette
Out of habit, I hold forks differently, and I could just leave it at that. But today let's take option B: indisputable proof that my way is superior.
The problem with the "proper" way to hold a fork is that it's inefficient. How are you supposed to balance the torque on the fork? If you got food on one end of the fork, it applies an off-center force. Thus, it applies a torque. Without an equal and opposite torque, the fork will simply tip over, resulting in an etiquette catastrophe. Imagine all the gasps which will be pointed in your general direction.
The best way to apply an opposite torque is to apply a downward force on the handle of the fork. The amount of torque is proportional to the distance from the center of mass times the strength of the force. Thus, if you hold it the "proper" way, only holding the fork near the center, you must apply a much stronger downward force. This makes the fork seem much heavier than it really is.
Put in plainer words, what's that long handle for if you're not going to use it for extra leverage?
I suppose if this really becomes a problem, you're probably putting way more food on your fork than is polite...
How do I hold it, you ask? Erm... I do it in a way that gives me more leverage. Do not question this!
Next time, I will discuss why it is always better to break your egg on the larger end.
For example, I have the quirk that I hold forks and spoons in an improper way.
If you're holding a spoon or a fork alone, you're supposed to hold it with your thumb and index finger as it rests on the side of your middle finger. This really needs a picture, but unfortunately, the only one I could find is copyrighted, and I don't feel comfortable taking it. Hopefully, the lack of pictures on the net means that most people simply don't care about etiquette
Out of habit, I hold forks differently, and I could just leave it at that. But today let's take option B: indisputable proof that my way is superior.
The problem with the "proper" way to hold a fork is that it's inefficient. How are you supposed to balance the torque on the fork? If you got food on one end of the fork, it applies an off-center force. Thus, it applies a torque. Without an equal and opposite torque, the fork will simply tip over, resulting in an etiquette catastrophe. Imagine all the gasps which will be pointed in your general direction.
The best way to apply an opposite torque is to apply a downward force on the handle of the fork. The amount of torque is proportional to the distance from the center of mass times the strength of the force. Thus, if you hold it the "proper" way, only holding the fork near the center, you must apply a much stronger downward force. This makes the fork seem much heavier than it really is.
Put in plainer words, what's that long handle for if you're not going to use it for extra leverage?
I suppose if this really becomes a problem, you're probably putting way more food on your fork than is polite...
How do I hold it, you ask? Erm... I do it in a way that gives me more leverage. Do not question this!
Next time, I will discuss why it is always better to break your egg on the larger end.
Wednesday, January 7, 2009
The rotating spaceship
The trouble with space, among other things, is that there's no gravity.* Weightlessness is known to cause a variety of health effects, the most obvious being muscle atrophy. So how can we create an artificial gravity? There aren't really any other forces which behave quite like gravity, which always has a strength proportional to your mass. But wait, there's the centrifugal force! If you're on a large rotating spaceship, the centrifugal force is what flings you away from the center of rotation.
*Technically, there is still gravity if you're in orbit, but you can't feel it because an orbit is basically a free-fall trajectory.
At this point, I am obligated to defend my use of "centrifugal force". Some overzealous science teachers have insisted that there is no such thing as the "centrifugal force"; there is only the "centrifugal effects" and "centripetal acceleration". Take it from me, that is baloney. The centrifugal force is what we call a "fictitious force", a force that depends on our reference frame. But "fictitious" is a bit of a misnomer. Fictitious forces have effects that are equally real as any other force. It's also worth noting that under Einstein's General Relativity, gravity is also essentially a fictitious force. Gravity is still real, is it not? We're all physicists here, not solipsists!
This is Space Station V, as seen in 2001: A Space Odyssey. It is a fictional example of a spaceship which harnesses the centrifugal force to create artificial gravity. No real examples exist, not yet. On the Space Station V, there are two independently rotating wheels. Unless any rocket fuel is expended, angular momentum (which is a measure of rotation) is a conserved quantity. Therefore, to preserve fuel, the spaceship would have an overall angular momentum of zero. Therefore, the space station is built so that the two wheels rotate in opposite directions, canceling each other's angular momentum.
[ETA: They also could use fuel to make the entire space station rotate in the same direction. I'm not sure which is the case for Space Station V.]
To consider the physics of the spaceship, let us consider just one of the wheels, and consider a rotating reference frame. It is important to remember that a rotating reference frame is not an inertial reference frame. That means that Newton's Laws do not apply! An object at rest does not necessarily remain at rest. Not every force is necessarily accompanied by an equal and opposite force. How can we even make sense of the physics of our rotating reference frame? It turns out that we can make sense of it rather easily. We simply need to assume that a new force, the centrifugal force, is acting on all objects. The centrifugal force pushes all objects outwards, away from the center of rotation.
This situation should make sense in both the rotating reference frame and the stationary reference frame.
Image not to scale
The Coriolis force works on all objects which appear to be moving in the rotating reference frame. That's why we didn't have to include it when we were talking about the astronaut inside the spaceship--he was stationary with respect to the rotating spaceship. The force does not always pull you inwards, but it is always perpendicular to the object's motion. Let's say you are inside the spaceship, facing the direction of rotation. If you run forward, you will feel heavier. If you run backwards, you will feel lighter. And this is a little harder to imagine: if you jump up, the Coriolis force pushes you slightly forward, and when you fall back down the Coriolis force pushes you slightly backwards.
If that made any sense, you can congratulate yourself for successfully performing a thought experiment, in very much the same spirit as Albert Einstein. If it didn't make any sense, it's probably my fault, and you can ask me in the comments. :)
*Technically, there is still gravity if you're in orbit, but you can't feel it because an orbit is basically a free-fall trajectory.
At this point, I am obligated to defend my use of "centrifugal force". Some overzealous science teachers have insisted that there is no such thing as the "centrifugal force"; there is only the "centrifugal effects" and "centripetal acceleration". Take it from me, that is baloney. The centrifugal force is what we call a "fictitious force", a force that depends on our reference frame. But "fictitious" is a bit of a misnomer. Fictitious forces have effects that are equally real as any other force. It's also worth noting that under Einstein's General Relativity, gravity is also essentially a fictitious force. Gravity is still real, is it not? We're all physicists here, not solipsists!
This is Space Station V, as seen in 2001: A Space Odyssey. It is a fictional example of a spaceship which harnesses the centrifugal force to create artificial gravity. No real examples exist, not yet. On the Space Station V, there are two independently rotating wheels. Unless any rocket fuel is expended, angular momentum (which is a measure of rotation) is a conserved quantity. Therefore, to preserve fuel, the spaceship would have an overall angular momentum of zero. Therefore, the space station is built so that the two wheels rotate in opposite directions, canceling each other's angular momentum.[ETA: They also could use fuel to make the entire space station rotate in the same direction. I'm not sure which is the case for Space Station V.]
To consider the physics of the spaceship, let us consider just one of the wheels, and consider a rotating reference frame. It is important to remember that a rotating reference frame is not an inertial reference frame. That means that Newton's Laws do not apply! An object at rest does not necessarily remain at rest. Not every force is necessarily accompanied by an equal and opposite force. How can we even make sense of the physics of our rotating reference frame? It turns out that we can make sense of it rather easily. We simply need to assume that a new force, the centrifugal force, is acting on all objects. The centrifugal force pushes all objects outwards, away from the center of rotation.
This situation should make sense in both the rotating reference frame and the stationary reference frame.
- Rotating reference frame: The centrifugal force pushes astronauts outwards, but the floor of the spaceship keeps him from being flung away.
- Stationary reference frame: The astronaut is circling around inside the rotating spaceship. He would continue flying in a straight line away from the spaceship, except the floor is stopping him.
Image not to scale- Stationary reference frame: The spaceship is rotating, but the astronaut is not rotating with it. No forces are acting on him, so he remains stationary just outside the spaceship.
- Rotating reference frame: The astronaut is circling the spaceship. The centrifugal force is pushing him outwards, and yet, he remains in the circular path. How?
The answer is that there are not one but two fictitious forces associated with a rotating reference frame. We have the centrifugal force, which pushes the astronaut outwards, and the Coriolis force, which pushes the astronaut inwards. You can all breathe a sigh of relief--we haven't broken physics after all.
The Coriolis force works on all objects which appear to be moving in the rotating reference frame. That's why we didn't have to include it when we were talking about the astronaut inside the spaceship--he was stationary with respect to the rotating spaceship. The force does not always pull you inwards, but it is always perpendicular to the object's motion. Let's say you are inside the spaceship, facing the direction of rotation. If you run forward, you will feel heavier. If you run backwards, you will feel lighter. And this is a little harder to imagine: if you jump up, the Coriolis force pushes you slightly forward, and when you fall back down the Coriolis force pushes you slightly backwards.
If that made any sense, you can congratulate yourself for successfully performing a thought experiment, in very much the same spirit as Albert Einstein. If it didn't make any sense, it's probably my fault, and you can ask me in the comments. :)
Friday, August 1, 2008
The myth of the toilet drain
Can you tell if I've flipped this picture?Have you ever heard that toilets in the northern hemisphere drain in one direction while those in the southern hemisphere drain in opposite direction? It's not true. Who knows why people think it is. It's sort of a harmless myth, a little science factoid that people enjoy perpetuating. I guess it just isn't terribly important to most people whether these science factoids are true or not. Though it's as harmless as they come, debunking this myth is fun, because I get to talk about some real science in the process.
The Coriolis Force
Supposedly, the reason that the water drains one way rather than the other is because of the Coriolis force. The Coriolis force is a "fictitious" force that appears when you consider a rotating reference frame, such as a point on Earth's rotating surface. By "fictitious", we don't mean it's not real. That just means that it appears in one reference frame, but not another. In more advanced theories, gravity is considered a fictitious force too, since it disappears when you consider a free-falling reference frame such as a space-station in orbit.
So what causes this Coriolis force? Usually, an object will move in a straight line unless there are some external forces changing its direction. But in a rotating reference frame, we would expect the direction to rotate along with the frame. Thus, when an object is moving, the Coriolis force causes it to slowly change its direction.* In the northern hemisphere, a moving object will slowly turn right. In the southern hemisphere, a moving object will slowly turn left. The further away from the equator, the more quickly it turns. This has to do with the orientation of earth's surface relative to the axis of rotation.
The reason the Coriolis force does not affect a toilet is because it's far too weak. Think about how slowly the Earth turns. That's right, it takes a whole day to make a complete rotation! Unless the toilet takes a whole day to drain, the Coriolis force can have hardly any effect at all. It will be extremely small in comparison to other effects like the shape of the toilet bowl, or the direction of the water as it comes in. On the other hand, the Coriolis force has a huge effect on ocean and air currents, as well as the direction of hurricanes, since all these phenomena last much longer than a day.
That said, it is possible for the Coriolis force to determine the direction that a sink drains. You just need to have a highly symmetrical basin, and make sure that the water is not moving initially or anything. And then you need to let it drain for maybe several hours. It's not an easy experiment.
*This is just the short, lying-to-children explanation. To get the full picture, you have to include another fictitious force that can also affect the direction, called the centrifugal force. Only together do these forces change the magnitude and direction of the velocity in the correct manner.
The Vortex Direction
Time for a quiz. If the Coriolis force did have a large effect on toilets, which way would they drain in the northern hemisphere?
Initially, I thought it would drain clockwise, because the Coriolis force makes the path turn right, creating clockwise circles. But I was wrong! As the water begins draining towards the center, its path is deflected to the right. Then the water goes counter-clockwise around the drain, because the Coriolis force is balanced by the force of water pressure. This really needs an illustration:
Image from Bad Science's Bad Coriolis FAQ. Cf (red) indicates the direction of the Coriolis force, while pgf (purple) indicates the direction of water pressure.The direction actually depends on whether the center of the vortex is low pressure (such as a drain or a hurricane) or high pressure. In the absence of a vortex, I think the body of water or air will rotate clockwise according to my previous analysis.
As for the picture at the beginning, it's true, I flipped it. No, you can't tell which hemisphere it's from.
Wednesday, July 2, 2008
Home experiment: Spinning box
Here's a physics experiment that you can try yourself right now. It's fun, I promise.
First, you have to find a small rectangularly-shaped object. Nothing valuable or breakable. A box works fine. A book works too, but you may have to tape the book shut for best results. It is important that there are no square sides on the object. All sides must be rectangles!
Here's my 3-d model of the box (created with Mathematica). Your own box might differ slightly in its shape, but it should be more or less the same. What are those sticks, you ask? They're just imaginary lines I drew to mark the three principal axes. If you have an object like a cube or a sphere, one axis is as good as another. But for an object shaped like above, there are three special axes of rotation, called the principal axes.
Now, take the box and toss it up into the air. Give it some spin as you toss it. First, make it spin around the blue line, then the green line, and then the red line.* Observe any differences between the three. I will wait.
...
The first thing you should notice is that it's harder to spin the box around some axes than others. It should take the most work to spin it around the green line, and the least work to spin it around the blue line. This is because the green axis has the greatest moment of inertia. The blue axis has the smallest moment of inertia. The red axis is somewhere in-between.
The other thing you should observe is that when you try spinning around the red axis, the box spins in a really odd way. After you let go of the box, it will not simply spin around the red axis, but spin and flip around in unexpected ways. If you draw a big "M" on the box, sometimes it will flip around so that you see a "W".
Why does it do this? The reason is because the principal axes with the greatest and smallest moments of inertia are stable. That is, if you spin around these axes, the object will continue to spin in more or less the same direction, even if you didn't spin it in exactly the right way. However, the principal axis with the middle moment of inertia is unstable. If you didn't spin it in exactly the right way, or if air friction pushes the box just a little bit, it will start spinning in all sorts of weird directions.
It's sort of like carrying a handbag. It's easy to hang it over your arm, because that is a stable position. But it's difficult to balance it on your head because that is an unstable position. Stability and instability are important concepts if you want to think like a physicist.
As for why two of the principal axes are stable and the other is not, that is a difficult question with a very mathematical answer. It has to do with three equations called Euler's Equations.
They are a mathematical consequence of Newton's Laws. I know many of you are looking at that and thinking, "Those equations look so ridiculously complicated!" In this case, you are absolutely right--these equations are ridiculously complicated, even after you learn about differential equations. But even if we don't solve the equations completely, we can still make qualitative predictions. If you have a cubical or spherical object, its rotation will remain constant. If you have a weirdly shaped object like your box, its rotation is stable around the principal axes of smallest and largest moments of inertia, but unstable around the third principal axis. By testing those predictions, you've just done some science!
*For the colorblind: blue goes from upper-left to lower-right, green is vertical, and red goes from lower-left to upper-right.
First, you have to find a small rectangularly-shaped object. Nothing valuable or breakable. A box works fine. A book works too, but you may have to tape the book shut for best results. It is important that there are no square sides on the object. All sides must be rectangles!
Here's my 3-d model of the box (created with Mathematica). Your own box might differ slightly in its shape, but it should be more or less the same. What are those sticks, you ask? They're just imaginary lines I drew to mark the three principal axes. If you have an object like a cube or a sphere, one axis is as good as another. But for an object shaped like above, there are three special axes of rotation, called the principal axes.Now, take the box and toss it up into the air. Give it some spin as you toss it. First, make it spin around the blue line, then the green line, and then the red line.* Observe any differences between the three. I will wait.
...
The first thing you should notice is that it's harder to spin the box around some axes than others. It should take the most work to spin it around the green line, and the least work to spin it around the blue line. This is because the green axis has the greatest moment of inertia. The blue axis has the smallest moment of inertia. The red axis is somewhere in-between.
The other thing you should observe is that when you try spinning around the red axis, the box spins in a really odd way. After you let go of the box, it will not simply spin around the red axis, but spin and flip around in unexpected ways. If you draw a big "M" on the box, sometimes it will flip around so that you see a "W".
Why does it do this? The reason is because the principal axes with the greatest and smallest moments of inertia are stable. That is, if you spin around these axes, the object will continue to spin in more or less the same direction, even if you didn't spin it in exactly the right way. However, the principal axis with the middle moment of inertia is unstable. If you didn't spin it in exactly the right way, or if air friction pushes the box just a little bit, it will start spinning in all sorts of weird directions.
It's sort of like carrying a handbag. It's easy to hang it over your arm, because that is a stable position. But it's difficult to balance it on your head because that is an unstable position. Stability and instability are important concepts if you want to think like a physicist.
As for why two of the principal axes are stable and the other is not, that is a difficult question with a very mathematical answer. It has to do with three equations called Euler's Equations.
They are a mathematical consequence of Newton's Laws. I know many of you are looking at that and thinking, "Those equations look so ridiculously complicated!" In this case, you are absolutely right--these equations are ridiculously complicated, even after you learn about differential equations. But even if we don't solve the equations completely, we can still make qualitative predictions. If you have a cubical or spherical object, its rotation will remain constant. If you have a weirdly shaped object like your box, its rotation is stable around the principal axes of smallest and largest moments of inertia, but unstable around the third principal axis. By testing those predictions, you've just done some science!*For the colorblind: blue goes from upper-left to lower-right, green is vertical, and red goes from lower-left to upper-right.
Friday, May 16, 2008
Bouncing electrons (Part 2)
See Part 1
When we last stopped, I had shown that electrons move along magnetic field lines. But if they simply follow the magnetic field lines, they'll eventually hit the Earth. Some do hit the earth, but others actually bounce back in a process called "magnetic mirroring". Why is this?
Ok, so I'm using the same picture. This time, I want you to notice that near the poles, the lines are very close together. The lines spread out much more when they are far away from the earth. When the lines are closer together, this means the magnetic field is stronger. When they are further apart, it means the magnetic field is weaker. It should come as no surprise that Earth's magnetic field is strongest when you are close to Earth.
This is a bit of an oversimplification, but the basic idea is that stronger magnetic fields repel electrons.* Therefore, if an electron is traveling along a magnetic field line, getting closer to Earth's north pole, it will eventually turn around. And then it will follow the magnetic field line all the way to the south pole. But since the magnetic field is stronger near the south pole, the electron will turn around again. As a result, electrons will bounce back and forth from pole to pole. Each bounce happens in a matter of seconds.
One of the results of this bouncing is that some regions of Earth's magnetic field are like traps for electrons (as well as other charged particles). And so we have the Van Allen Radiation belts, where lots of high energy radiation is trapped. Their shape can be described as "toroidal" or "donut-shaped". There are several other important regions above Earth with similar shapes.
Mmmm... radiation donuts.
Ok, so electrons are doing two things at once. They are gyrating and bouncing from pole to pole. But that's not all!
There is a third type of motion caused by Earth's gravity. Electrons, though very light particles, still fall. Only they don't fall. Remember, they're still trapped on magnetic field lines. If they fall down, they will very quickly circle around back up. So perhaps gravity has no effect at all? But it does have an effect! Unlike the magnetic field, gravity actually slows down and speeds up electrons instead of simply changing their direction. And faster electrons make larger circles! One side of the circle (the one closer to Earth) will be larger while the other side will be smaller. The resulting motion will look something like this.
As weird as it sounds, downward gravity causes the electron to "drift" to the side! Specifically, electrons will drift eastward. It takes a few minutes for them to go all the way around the Earth. Positively charged particles will also drift, but in the westward direction. Negative charges drift east, positive charges drift west, and we've got an electric current! This is called the ring current. Scientists measure the ring current to determine how many particles are in space, which tells us something about how the "space weather" is going.
And so, electrons above Earth have three types of motion. They gyrate, making hundreds of circles every second. They bounce from north pole to south pole in a matter of seconds. They drift eastward, going around the earth in a few minutes.
There's one last detail I want to add (and there are always more details), because it is related what I researched. All of the above types of motion conserve energy. The electron doesn't really change its speed much. However, this assumes that Earth's magnetic field is constant. It isn't. A stream of particles called the solar wind is always coming out from the sun. When these particles hit the Earth's magnetic field, they cause the magnetic field lines to vibrate like harp strings. Now, each of the three types of motion occurs at a different frequency. If the harp strings vibrate at a frequency near one of the types of motion, a resonant interaction will occur! For example, if the magnetic field line fluctuates every few minutes, it will resonate with the drift motion. The electrons might move between field lines, or speed up. We think this is the cause of one of the Van Allen Radiation Belts, but we're not sure. To find out, we must take lots of data in various circumstances to see if the evidence all lines up!
*Electrons don't actually slow down when moving into stronger electric fields, they simply transfer some of their forward motion to their circling motion. The technical description of this is that electrons conserve their "magnetic moment" under ordinary conditions.
When we last stopped, I had shown that electrons move along magnetic field lines. But if they simply follow the magnetic field lines, they'll eventually hit the Earth. Some do hit the earth, but others actually bounce back in a process called "magnetic mirroring". Why is this?
Ok, so I'm using the same picture. This time, I want you to notice that near the poles, the lines are very close together. The lines spread out much more when they are far away from the earth. When the lines are closer together, this means the magnetic field is stronger. When they are further apart, it means the magnetic field is weaker. It should come as no surprise that Earth's magnetic field is strongest when you are close to Earth.This is a bit of an oversimplification, but the basic idea is that stronger magnetic fields repel electrons.* Therefore, if an electron is traveling along a magnetic field line, getting closer to Earth's north pole, it will eventually turn around. And then it will follow the magnetic field line all the way to the south pole. But since the magnetic field is stronger near the south pole, the electron will turn around again. As a result, electrons will bounce back and forth from pole to pole. Each bounce happens in a matter of seconds.
One of the results of this bouncing is that some regions of Earth's magnetic field are like traps for electrons (as well as other charged particles). And so we have the Van Allen Radiation belts, where lots of high energy radiation is trapped. Their shape can be described as "toroidal" or "donut-shaped". There are several other important regions above Earth with similar shapes.
Mmmm... radiation donuts.Ok, so electrons are doing two things at once. They are gyrating and bouncing from pole to pole. But that's not all!
There is a third type of motion caused by Earth's gravity. Electrons, though very light particles, still fall. Only they don't fall. Remember, they're still trapped on magnetic field lines. If they fall down, they will very quickly circle around back up. So perhaps gravity has no effect at all? But it does have an effect! Unlike the magnetic field, gravity actually slows down and speeds up electrons instead of simply changing their direction. And faster electrons make larger circles! One side of the circle (the one closer to Earth) will be larger while the other side will be smaller. The resulting motion will look something like this.
As weird as it sounds, downward gravity causes the electron to "drift" to the side! Specifically, electrons will drift eastward. It takes a few minutes for them to go all the way around the Earth. Positively charged particles will also drift, but in the westward direction. Negative charges drift east, positive charges drift west, and we've got an electric current! This is called the ring current. Scientists measure the ring current to determine how many particles are in space, which tells us something about how the "space weather" is going.And so, electrons above Earth have three types of motion. They gyrate, making hundreds of circles every second. They bounce from north pole to south pole in a matter of seconds. They drift eastward, going around the earth in a few minutes.
There's one last detail I want to add (and there are always more details), because it is related what I researched. All of the above types of motion conserve energy. The electron doesn't really change its speed much. However, this assumes that Earth's magnetic field is constant. It isn't. A stream of particles called the solar wind is always coming out from the sun. When these particles hit the Earth's magnetic field, they cause the magnetic field lines to vibrate like harp strings. Now, each of the three types of motion occurs at a different frequency. If the harp strings vibrate at a frequency near one of the types of motion, a resonant interaction will occur! For example, if the magnetic field line fluctuates every few minutes, it will resonate with the drift motion. The electrons might move between field lines, or speed up. We think this is the cause of one of the Van Allen Radiation Belts, but we're not sure. To find out, we must take lots of data in various circumstances to see if the evidence all lines up!
*Electrons don't actually slow down when moving into stronger electric fields, they simply transfer some of their forward motion to their circling motion. The technical description of this is that electrons conserve their "magnetic moment" under ordinary conditions.
Wednesday, May 14, 2008
Bouncing electrons (Part 1)
An electron is simply a very light particle with a negative charge. Usually, they're paired up with atoms, and they give us the full range of chemical reactions. But when electrons are by themselves, they're not really all that complicated, are they? In fact, above Earth's atmosphere, there are plenty of electrons all by themselves. Of course, by "plenty" I mean a near-perfect vacuum, but it's a lot by empty-space standards. There aren't really enough for them to bump into themselves very often. So what could they possibly do besides float leisurely in space?
It turns out that electrons do a lot, because they interact with Earth's magnetic field.
Magnetic fields, if you didn't know, are different from electric fields. Sometimes people get the electric force and magnetic force mixed up because on the surface they're so similar. The electric force, (which manifests in lightning and static electricity) causes like charges to repel and opposite charges to attract. Similarly, the magnetic force (which manifests in magnets and compasses) causes like poles to repel and opposite poles to attract. But magnetic poles do not attract or repel electric charges. They have a much stranger interaction.
The way that magnets work is by creating a magnetic field. The field consists of invisible lines that go from the north pole to the south pole. Technically, Earth's north magnetic pole is actually in the southern hemisphere, so sometimes "north" and "south" are mixed up (to the dismay of geophysicists).
When electrons, or any charged particles, move through the magnetic field, the magnetic field pushes them in a direction that is perpendicular to their motion and perpendicular to the magnetic field. Since the electron is being pushed neither forward nor backwards, it doesn't speed up or slow down. Instead, it simply changes direction, and travels around in circles. This type of motion is called "gyration".
The arrow V shows which direction that the electron (light blue dot) is going. The arrow F shows which way the magnetic field is pushing the electron. Because F is always perpendicular to V, the electron will constantly change directions and travel in the circular green path. The magnetic field in this example is coming out of the screen towards you.
Now, personally, I think it's just amazing that this weird physical force causes electrons to move around in circles of all things (even more amazing when you find that it is a consequence of Relativity). Another weird consequence is that the electron make circles at the same rate, no matter how fast it's going. If it's going really fast, it will simply make larger circles. In Earth's magnetic field, electrons will make hundreds of circles per second, regardless of their speed. This rate is known as the cyclotron frequency.
The electron cannot get too far away from the magnetic field line because it will simply circle back on itself instead. However, it can travel along the magnetic field lines without any resistance at all. The result is that the electrons are free to move along the magnetic field lines (in helix-shaped paths), but cannot jump from one line to another. It turns out that those invisible magnetic field lines aren't just mathematical curiosities, but they actually tell us where the electrons can move.
So where do the electrons end up? If you follow the magnetic field lines, don't they simply hit the earth? Yes, they do! Some of those particles will hit the upper atmosphere, creating colorful displays of light: the aurora. That's why the aurora is most common near the north and south poles--because that's where most of the particles come down and hit the atmosphere.
But not all of the particles hit the earth. Some of them "bounce" back along the magnetic field line! Find out why in Part 2.
It turns out that electrons do a lot, because they interact with Earth's magnetic field.
Magnetic fields, if you didn't know, are different from electric fields. Sometimes people get the electric force and magnetic force mixed up because on the surface they're so similar. The electric force, (which manifests in lightning and static electricity) causes like charges to repel and opposite charges to attract. Similarly, the magnetic force (which manifests in magnets and compasses) causes like poles to repel and opposite poles to attract. But magnetic poles do not attract or repel electric charges. They have a much stranger interaction.
The way that magnets work is by creating a magnetic field. The field consists of invisible lines that go from the north pole to the south pole. Technically, Earth's north magnetic pole is actually in the southern hemisphere, so sometimes "north" and "south" are mixed up (to the dismay of geophysicists).
When electrons, or any charged particles, move through the magnetic field, the magnetic field pushes them in a direction that is perpendicular to their motion and perpendicular to the magnetic field. Since the electron is being pushed neither forward nor backwards, it doesn't speed up or slow down. Instead, it simply changes direction, and travels around in circles. This type of motion is called "gyration".
The arrow V shows which direction that the electron (light blue dot) is going. The arrow F shows which way the magnetic field is pushing the electron. Because F is always perpendicular to V, the electron will constantly change directions and travel in the circular green path. The magnetic field in this example is coming out of the screen towards you.Now, personally, I think it's just amazing that this weird physical force causes electrons to move around in circles of all things (even more amazing when you find that it is a consequence of Relativity). Another weird consequence is that the electron make circles at the same rate, no matter how fast it's going. If it's going really fast, it will simply make larger circles. In Earth's magnetic field, electrons will make hundreds of circles per second, regardless of their speed. This rate is known as the cyclotron frequency.
The electron cannot get too far away from the magnetic field line because it will simply circle back on itself instead. However, it can travel along the magnetic field lines without any resistance at all. The result is that the electrons are free to move along the magnetic field lines (in helix-shaped paths), but cannot jump from one line to another. It turns out that those invisible magnetic field lines aren't just mathematical curiosities, but they actually tell us where the electrons can move.
So where do the electrons end up? If you follow the magnetic field lines, don't they simply hit the earth? Yes, they do! Some of those particles will hit the upper atmosphere, creating colorful displays of light: the aurora. That's why the aurora is most common near the north and south poles--because that's where most of the particles come down and hit the atmosphere.
But not all of the particles hit the earth. Some of them "bounce" back along the magnetic field line! Find out why in Part 2.
Friday, May 2, 2008
Motorcycle physics
Some one I know has a motorcycle, and he told me that it's much more difficult to drive than a car. Furthermore, in order to turn right, you push the right handlebar. Counterintuitive, huh? I was puzzling over this for about a month, trying to figure out how this was physically possible. After all, shouldn't the wheel turn to the left if you push right?
Well, I've finally got my answer! The wheel is precessing!
To visualize this, imagine that you are sitting on a motorcycle. The motorcycle must be moving very quickly, much faster than a bicycle. If it were moving at the same speed as a regular bike, then pushing right would indeed cause the wheel to turn left. But if the wheel is spinning very quickly, there will be too much energy invested in rotation for the wheel to simply turn like a bicycle's wheel.
The wheel of the motorcycle is spinning forward. This corresponds to an angular momentum going to your left. When you push on the right handle bar, you apply torque in the upwards direction. The angular momentum changes in the direction of the torque, tilting upwards. As a result, the entire spinning wheel will lean to the right. Thus, you turn right by pushing right.
Precession: not just for physics demonstrations!
Well, I've finally got my answer! The wheel is precessing!
To visualize this, imagine that you are sitting on a motorcycle. The motorcycle must be moving very quickly, much faster than a bicycle. If it were moving at the same speed as a regular bike, then pushing right would indeed cause the wheel to turn left. But if the wheel is spinning very quickly, there will be too much energy invested in rotation for the wheel to simply turn like a bicycle's wheel.
The wheel of the motorcycle is spinning forward. This corresponds to an angular momentum going to your left. When you push on the right handle bar, you apply torque in the upwards direction. The angular momentum changes in the direction of the torque, tilting upwards. As a result, the entire spinning wheel will lean to the right. Thus, you turn right by pushing right.
Precession: not just for physics demonstrations!
Sunday, April 20, 2008
The principle of least action
Earlier, I spoke of the philosophy of Lagrangian mechanics. I got at least one person interested in learning more. I guess philosophy isn't completely useless after all!
The story of Lagrangian mechanics, in a way, starts with the brachistochrone problem. In 1696, one of the Bournoulli brothers challenged the mathematicians of the world with this problem: Given two points A and B, what curve will result in an object rolling from A to B in the shortest amount of time? Hint: it's not a straight line! The story goes that Isaac Newton solved this problem within a day, and invented a whole new branch of calculus (called the calculus of variations) to do so! Newton was just that kind of guy.
I'm not going to solve the entire problem here, as it's rather difficult, but I'll outline the general idea. See, the amount of time that the object takes to roll is equal to distance divided by velocity. Of course, the velocity is not always constant, so we have to think about in calculus terms.
Bournoulli had his own answer to the problem, and it used quite a different method. He used something called Fermat's principle, which states that the path light takes from A to B is the path that takes the least amount of time. Of course, light isn't a normal object that can roll down inclines, but it can be slowed down when it goes through certain types of materials. Just as on object can be slowed down by rolling it up a cliff, light can be slowed down by the appropriate use of materials. If you set it up right, light will travel along the solution to the brachistochrone problem!
It turns out that the solution is a cycloid, which is the same curve traced out by a nail that gets stuck in a tire.
How does this all relate to Lagrangian mechanics? Just like Fermat's principle, Lagrangian mechanics states that the path an object takes from A to B also minimizes something. That quantity which is minimized is called "action".
The story of Lagrangian mechanics, in a way, starts with the brachistochrone problem. In 1696, one of the Bournoulli brothers challenged the mathematicians of the world with this problem: Given two points A and B, what curve will result in an object rolling from A to B in the shortest amount of time? Hint: it's not a straight line! The story goes that Isaac Newton solved this problem within a day, and invented a whole new branch of calculus (called the calculus of variations) to do so! Newton was just that kind of guy.
I'm not going to solve the entire problem here, as it's rather difficult, but I'll outline the general idea. See, the amount of time that the object takes to roll is equal to distance divided by velocity. Of course, the velocity is not always constant, so we have to think about in calculus terms.
T = ∫ dx/v
For those who are afraid of math, don't worry. This is just a fancy way of saying time (T) is distance (dx) divided by velocity (v). The difficult part is that the velocity is a complicated function involving both the shape of the curve and how far we've gone on that curve. And there are infinitely many possible curves. How do we pick the best one? Newton's answer came from the calculus of variations. Unfortunately, this is impossible to show without assuming my readers have a ton of calculus background. I'll spare you!Bournoulli had his own answer to the problem, and it used quite a different method. He used something called Fermat's principle, which states that the path light takes from A to B is the path that takes the least amount of time. Of course, light isn't a normal object that can roll down inclines, but it can be slowed down when it goes through certain types of materials. Just as on object can be slowed down by rolling it up a cliff, light can be slowed down by the appropriate use of materials. If you set it up right, light will travel along the solution to the brachistochrone problem!
It turns out that the solution is a cycloid, which is the same curve traced out by a nail that gets stuck in a tire.
How does this all relate to Lagrangian mechanics? Just like Fermat's principle, Lagrangian mechanics states that the path an object takes from A to B also minimizes something. That quantity which is minimized is called "action".
S = ∫ L dt
Here, S represents the action. Action is equal to the Lagrangian (L) multiplied by time (dt). The Lagrangian is a special quantity that will tell you almost everything you need to know about a physical system in order to predict its future. In a simple system, the Lagrangian is equal to the kinetic energy minus the potential energy.
Let's consider a simple example. I throw a ball up and catch it. The ball is moving from point A (my hand) to point B (my other hand). To minimize action, the ball will "try" to have a high potential energy for as long as possible. To do so, it will soar up into the air. But it will not go too high, because then it would have to move fast to come down in time to land in my other hand. The faster it moves, the higher its kinetic energy, and the higher its action. Therefore, the ball will go up high, but not too high. The result is a parabolic path.
You can see why Lagrangian mechanics seem to imbue physical laws with a sense of purpose. The ball "tries" to minimize action as it goes from here to there. It even seems to foresee into the future, carefully plotting the course that will have the least action in the long run. Well, perhaps it only has foresight because we've already told the ball exactly where it will end up--in my hand at point B.
I think this philosophical side is part of the reason that physicists originally thought up Lagrangian mechanics. Perhaps it would disappoint the original physicists to know that action is not necessarily minimized, except in the simplest of cases. Sometimes it's maximized, or it's on a "saddle point". Try philosophizing that.
When we actually work with Lagrangian mechanics, we don't use this fanciful thought process at all. We use the calculus of variations and the Euler-Lagrange equation. For a simple problem, this will result in the equation F = ma. The equations are the real motivation behind Lagrangian mechanics, not the philosophy, but the philosophy is fun to consider.
Let's consider a simple example. I throw a ball up and catch it. The ball is moving from point A (my hand) to point B (my other hand). To minimize action, the ball will "try" to have a high potential energy for as long as possible. To do so, it will soar up into the air. But it will not go too high, because then it would have to move fast to come down in time to land in my other hand. The faster it moves, the higher its kinetic energy, and the higher its action. Therefore, the ball will go up high, but not too high. The result is a parabolic path.
You can see why Lagrangian mechanics seem to imbue physical laws with a sense of purpose. The ball "tries" to minimize action as it goes from here to there. It even seems to foresee into the future, carefully plotting the course that will have the least action in the long run. Well, perhaps it only has foresight because we've already told the ball exactly where it will end up--in my hand at point B.
I think this philosophical side is part of the reason that physicists originally thought up Lagrangian mechanics. Perhaps it would disappoint the original physicists to know that action is not necessarily minimized, except in the simplest of cases. Sometimes it's maximized, or it's on a "saddle point". Try philosophizing that.
When we actually work with Lagrangian mechanics, we don't use this fanciful thought process at all. We use the calculus of variations and the Euler-Lagrange equation. For a simple problem, this will result in the equation F = ma. The equations are the real motivation behind Lagrangian mechanics, not the philosophy, but the philosophy is fun to consider.
Saturday, April 12, 2008
Cosmic purpose and the Lagrangian
In my recent studies of physics, we learned about Lagrangian equations of motion. Now, unless you study physics, these equations would seem rather dry. They help me solve problems like the double pendulum, but they do so with purely mathematical equations. So as much as I know you'd all like to see the math, I will instead talk about the philosophy of Lagrangian dynamics.
"Philosophy?" you exclaim with bewilderment. Well, this subject was not entirely unprovoked. My text book has a paragraph, where it starts waxing metaphysical about how in Lagrangian dynamics, nature tries to achieve a certain purpose (emphasis not mine). I thought this paragraph was just hilarious.
To understand this point, I must explain what this "Lagrangian" thing is. Basically, Lagrangian mechanics is an alternative to Newtonian mechanics.
Newtonian mechanics is based on the equation F = ma. That is, force is equal to mass times acceleration. If I push something, it changes how fast it's going. So if we know exactly what forces are acting on an object, we can, in theory, determine where it will go. Of course, in practice, this is very difficult. What if the force depends on the location of the object (which is in turn affected by the force)? After some point, the math becomes hard. I don't mean this in the sense of, "Math is hard! Let's go shopping!" I mean that some of this math is impossible to solve, or near impossible. And if you're lucky, you can prove that it's impossible. That is why physicists try to simplify everything, wherever possible.
One of the ways to simplify Newtonian mechanics is by using Lagrangian mechanics instead. Lagrangian mechanics is more advanced (which is why they don't teach it in introductory physics), but mathematically cleaner. Instead of F = ma, Lagrangian mechanics states that action is minimized. Now, before the Daoists start jumping all over that one, I have to qualify the word "action." "Action" is a technical term for a particular quantity, the details of which are not covered in the scope of this post. To determine the path an object will take, you consider every possible path, and find the one path in which this quantity, action, is minimized. It sounds complicated, but it actually makes a variety of problems much simpler. Lagrangian mechanics is equivalent to Newtonian mechanics--it will always give you the same result, and you can prove it.
Back to my textbook. My textbook simply states that while the Newtonian and Lagrangian are mathematically equivalent, they are not philosophically equivalent. These philosophical implications have historically had profound influence on the development of mechanics.
So what are these philosophical differences? According to Newtonian mechanics, the world is viewed in terms of cause and effect. You push something, it moves. According to Lagrangian mechanics, the laws of physics are produced because nature is trying to achieve a purpose--to minimize action. An object has many possible paths, but the actual path is the one with the least action.
What are the implications for philosophy? Does it mean that the universe is governed by cause and effect? Or is it trying to fulfill a purpose? Or is it both, or neither?
If you asked me, this is an indication that such questions are irrelevant. It doesn't matter whether there is cause and effect, or whether there is a cosmic purpose. Physics behaves the same either way. If you can change the answers to these deep philosophical questions by simply moving around some mathematical equations, what meaning do these answers have?
Another layer of complication is the addition of another alternative to Newtonian mechanics: Hamiltonian Mechanics. As far as I can tell, Hamiltonian mechanics have no philosophical implications whatsoever. They're just a bunch of mathematical equations that make things simpler for physicists. Cosmic purpose is fleeting.
Has Lagrangian Mechanics piqued your interest? I wrote more.
"Philosophy?" you exclaim with bewilderment. Well, this subject was not entirely unprovoked. My text book has a paragraph, where it starts waxing metaphysical about how in Lagrangian dynamics, nature tries to achieve a certain purpose (emphasis not mine). I thought this paragraph was just hilarious.
To understand this point, I must explain what this "Lagrangian" thing is. Basically, Lagrangian mechanics is an alternative to Newtonian mechanics.
Newtonian mechanics is based on the equation F = ma. That is, force is equal to mass times acceleration. If I push something, it changes how fast it's going. So if we know exactly what forces are acting on an object, we can, in theory, determine where it will go. Of course, in practice, this is very difficult. What if the force depends on the location of the object (which is in turn affected by the force)? After some point, the math becomes hard. I don't mean this in the sense of, "Math is hard! Let's go shopping!" I mean that some of this math is impossible to solve, or near impossible. And if you're lucky, you can prove that it's impossible. That is why physicists try to simplify everything, wherever possible.
One of the ways to simplify Newtonian mechanics is by using Lagrangian mechanics instead. Lagrangian mechanics is more advanced (which is why they don't teach it in introductory physics), but mathematically cleaner. Instead of F = ma, Lagrangian mechanics states that action is minimized. Now, before the Daoists start jumping all over that one, I have to qualify the word "action." "Action" is a technical term for a particular quantity, the details of which are not covered in the scope of this post. To determine the path an object will take, you consider every possible path, and find the one path in which this quantity, action, is minimized. It sounds complicated, but it actually makes a variety of problems much simpler. Lagrangian mechanics is equivalent to Newtonian mechanics--it will always give you the same result, and you can prove it.
Back to my textbook. My textbook simply states that while the Newtonian and Lagrangian are mathematically equivalent, they are not philosophically equivalent. These philosophical implications have historically had profound influence on the development of mechanics.
So what are these philosophical differences? According to Newtonian mechanics, the world is viewed in terms of cause and effect. You push something, it moves. According to Lagrangian mechanics, the laws of physics are produced because nature is trying to achieve a purpose--to minimize action. An object has many possible paths, but the actual path is the one with the least action.
What are the implications for philosophy? Does it mean that the universe is governed by cause and effect? Or is it trying to fulfill a purpose? Or is it both, or neither?
If you asked me, this is an indication that such questions are irrelevant. It doesn't matter whether there is cause and effect, or whether there is a cosmic purpose. Physics behaves the same either way. If you can change the answers to these deep philosophical questions by simply moving around some mathematical equations, what meaning do these answers have?
Another layer of complication is the addition of another alternative to Newtonian mechanics: Hamiltonian Mechanics. As far as I can tell, Hamiltonian mechanics have no philosophical implications whatsoever. They're just a bunch of mathematical equations that make things simpler for physicists. Cosmic purpose is fleeting.
Has Lagrangian Mechanics piqued your interest? I wrote more.
Thursday, December 27, 2007
Precession explained
Forget precession for a moment. First, it's rotation explained!
When you rotate a three dimensional object, it always rotates around an imaginary line that we call the "axis of rotation". If the object we rotate is a wheel, then the axis of rotation goes through the axel. If you roll a spherical ball on the ground, the axis of rotation is perpendicular to the ball's path, and goes through the ball's center.
Well, if we want to know how "hard" it is to stop the object, then we need to find a certain value called "angular momentum". The angular momentum of any bit of matter is equal to its distance from the axis of rotation, times the mass, times how quickly it goes around the axis of rotation. Of course, your typical object is not a "bit" of matter, but an infinite number of bits of matter. To find the total angular momentum, we just sum up the angular momentum of all the little bits.
The problem with this simplistic view is that it ignores that objects can spin in many directions. To specify the direction of rotation, we say that the angular momentum goes in the same direction as the axis of rotation. If you look in the direction of angular momentum, the object will always appear to be rotating clockwise. If you rotate a standard screw, it moves in the direction of angular momentum.
Now, precession explained!
What is precession? Precession is when the axis of rotation itself spins. For example, when a gyroscope wobbles, its axis of rotation is first tilted north, then east, then south, and west. Its axis of rotation continues to change directions, moving around in a circle. It is important to remember that the axis of rotation is not in itself a physical object, so we would not expect it to spin unless there was some cool physics afoot. There is.
Angular momentum is just like regular motion: it does not change unless something pushes the object. In physics terms, we apply a force to the object. But force alone does not change angular momentum. For example, let's say we have a balance scale.
If we push straight down on the yellow circle, the two arms are not going to start rotating. However, if we push down on one of the arms, it will start moving. The further from the center we push, the less force it takes to move the scale.
The rate at which the angular momentum changes is equal to a value called "torque". Torque is equal to the amount of force times the distance from the axis of rotation. The reason it is easier to push the scale when further from the center is that it takes a smaller amount of force to create the same amount of torque. Torque, just like angular momentum, has a direction. If you apply torque, it will cause an object to change its angular momentum in the same direction as the torque you applied.
Now that we know about torque, let's look at a simple wheel with an axel. One end of the axel is hanging from a string. Excuse my poor art.
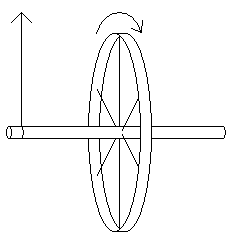In case it isn't clear, the wheel is rotating in the direction of the arrow in the middle, and the string is applying a force in the direction of the arrow on the left. The angular momentum of this wheel goes to the right.
Which way does the torque go? Well, if the wheel weren't spinning, then it would simply fall so that the axel is vertical. This fall would cause the wheel to spin clockwise from our point of view. Therefore, the torque is going into the page (forward, in the direction we are looking). This causes the angular momentum to move into the page.
However, once the angular momentum starts going into the page, the entire wheel turns. The direction of the torque has also turned, and is now facing left. The more the wheel turns, the more the direction of the torque turns. As a result, the angular momentum will perpetually go around in circles, chasing after the torque. And that's what causes precession.
Now, all of this is difficult to understand, except by resorting to math (yes, we were doing math, albeit simplified math). I can conceptually visualize special relativity, and the fourth dimension, but precession? That's hard. I believe that is the sentiment behind this comic strip from xkcd.
Next time: Precession as applied to Earth!
When you rotate a three dimensional object, it always rotates around an imaginary line that we call the "axis of rotation". If the object we rotate is a wheel, then the axis of rotation goes through the axel. If you roll a spherical ball on the ground, the axis of rotation is perpendicular to the ball's path, and goes through the ball's center.
Well, if we want to know how "hard" it is to stop the object, then we need to find a certain value called "angular momentum". The angular momentum of any bit of matter is equal to its distance from the axis of rotation, times the mass, times how quickly it goes around the axis of rotation. Of course, your typical object is not a "bit" of matter, but an infinite number of bits of matter. To find the total angular momentum, we just sum up the angular momentum of all the little bits.
The problem with this simplistic view is that it ignores that objects can spin in many directions. To specify the direction of rotation, we say that the angular momentum goes in the same direction as the axis of rotation. If you look in the direction of angular momentum, the object will always appear to be rotating clockwise. If you rotate a standard screw, it moves in the direction of angular momentum.
Now, precession explained!
What is precession? Precession is when the axis of rotation itself spins. For example, when a gyroscope wobbles, its axis of rotation is first tilted north, then east, then south, and west. Its axis of rotation continues to change directions, moving around in a circle. It is important to remember that the axis of rotation is not in itself a physical object, so we would not expect it to spin unless there was some cool physics afoot. There is.
Angular momentum is just like regular motion: it does not change unless something pushes the object. In physics terms, we apply a force to the object. But force alone does not change angular momentum. For example, let's say we have a balance scale.
If we push straight down on the yellow circle, the two arms are not going to start rotating. However, if we push down on one of the arms, it will start moving. The further from the center we push, the less force it takes to move the scale.The rate at which the angular momentum changes is equal to a value called "torque". Torque is equal to the amount of force times the distance from the axis of rotation. The reason it is easier to push the scale when further from the center is that it takes a smaller amount of force to create the same amount of torque. Torque, just like angular momentum, has a direction. If you apply torque, it will cause an object to change its angular momentum in the same direction as the torque you applied.
Now that we know about torque, let's look at a simple wheel with an axel. One end of the axel is hanging from a string. Excuse my poor art.
In case it isn't clear, the wheel is rotating in the direction of the arrow in the middle, and the string is applying a force in the direction of the arrow on the left. The angular momentum of this wheel goes to the right.Which way does the torque go? Well, if the wheel weren't spinning, then it would simply fall so that the axel is vertical. This fall would cause the wheel to spin clockwise from our point of view. Therefore, the torque is going into the page (forward, in the direction we are looking). This causes the angular momentum to move into the page.
However, once the angular momentum starts going into the page, the entire wheel turns. The direction of the torque has also turned, and is now facing left. The more the wheel turns, the more the direction of the torque turns. As a result, the angular momentum will perpetually go around in circles, chasing after the torque. And that's what causes precession.
Now, all of this is difficult to understand, except by resorting to math (yes, we were doing math, albeit simplified math). I can conceptually visualize special relativity, and the fourth dimension, but precession? That's hard. I believe that is the sentiment behind this comic strip from xkcd.
Next time: Precession as applied to Earth!
Subscribe to:
Posts (Atom)
