When you rotate a three dimensional object, it always rotates around an imaginary line that we call the "axis of rotation". If the object we rotate is a wheel, then the axis of rotation goes through the axel. If you roll a spherical ball on the ground, the axis of rotation is perpendicular to the ball's path, and goes through the ball's center.
Well, if we want to know how "hard" it is to stop the object, then we need to find a certain value called "angular momentum". The angular momentum of any bit of matter is equal to its distance from the axis of rotation, times the mass, times how quickly it goes around the axis of rotation. Of course, your typical object is not a "bit" of matter, but an infinite number of bits of matter. To find the total angular momentum, we just sum up the angular momentum of all the little bits.
The problem with this simplistic view is that it ignores that objects can spin in many directions. To specify the direction of rotation, we say that the angular momentum goes in the same direction as the axis of rotation. If you look in the direction of angular momentum, the object will always appear to be rotating clockwise. If you rotate a standard screw, it moves in the direction of angular momentum.
Now, precession explained!
What is precession? Precession is when the axis of rotation itself spins. For example, when a gyroscope wobbles, its axis of rotation is first tilted north, then east, then south, and west. Its axis of rotation continues to change directions, moving around in a circle. It is important to remember that the axis of rotation is not in itself a physical object, so we would not expect it to spin unless there was some cool physics afoot. There is.
Angular momentum is just like regular motion: it does not change unless something pushes the object. In physics terms, we apply a force to the object. But force alone does not change angular momentum. For example, let's say we have a balance scale.
If we push straight down on the yellow circle, the two arms are not going to start rotating. However, if we push down on one of the arms, it will start moving. The further from the center we push, the less force it takes to move the scale.The rate at which the angular momentum changes is equal to a value called "torque". Torque is equal to the amount of force times the distance from the axis of rotation. The reason it is easier to push the scale when further from the center is that it takes a smaller amount of force to create the same amount of torque. Torque, just like angular momentum, has a direction. If you apply torque, it will cause an object to change its angular momentum in the same direction as the torque you applied.
Now that we know about torque, let's look at a simple wheel with an axel. One end of the axel is hanging from a string. Excuse my poor art.
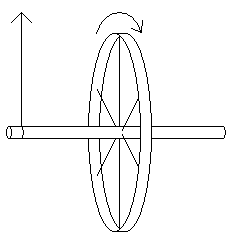In case it isn't clear, the wheel is rotating in the direction of the arrow in the middle, and the string is applying a force in the direction of the arrow on the left. The angular momentum of this wheel goes to the right.Which way does the torque go? Well, if the wheel weren't spinning, then it would simply fall so that the axel is vertical. This fall would cause the wheel to spin clockwise from our point of view. Therefore, the torque is going into the page (forward, in the direction we are looking). This causes the angular momentum to move into the page.
However, once the angular momentum starts going into the page, the entire wheel turns. The direction of the torque has also turned, and is now facing left. The more the wheel turns, the more the direction of the torque turns. As a result, the angular momentum will perpetually go around in circles, chasing after the torque. And that's what causes precession.
Now, all of this is difficult to understand, except by resorting to math (yes, we were doing math, albeit simplified math). I can conceptually visualize special relativity, and the fourth dimension, but precession? That's hard. I believe that is the sentiment behind this comic strip from xkcd.
Next time: Precession as applied to Earth!
