Mixed states
As I explained before, Quantum Mechanics implies that bound particles have discrete energy levels. If a particle is on one of these energy levels, we would say it is in a pure quantum state (or "eigenstate"). But there are more than just pure states in quantum mechanics. There are also mixed states, where a particle exists with two or more different energy levels all at once! We would call this a superposition of different energy states.
Superposition may sound really weird, but mathematically, it's not weird at all. Schrodinger's equation, the equation that defines quantum mechanics, has the property that if you take any two wavefunctions and add them together, you'll get another wavefunction. So if you take one wavefunction with energy E1 and another wavefunction with energy E2, and add them together, you get a mixed state which has a superposition of energy levels E1 and E2 simultaneously!
Everybody loves to hear about how weird quantum mechanics is, with particles being able to occupy multiple locations and have multiple energies, but do they realize that, mathematically, it's all just addition? Sometimes I think people who miss the math miss out.If you actually try to measure the energy of a mixed state, you are guaranteed to observe one and only one energy. If you have a particle that is partly in the E1 state and partly in the E2 state, the way we interpret that is that there is a certain probability of measuring E1 and a certain probability of measuring E2. As soon as we measure it, the particle changes into a pure state again. This is called wavefunction collapse, which is the doorway to many of the philosophical questions that loom around quantum mechanics. Wait, I've already talked about this before.
A bit of math (only a little, I promise)
Let's say we have a mixed state. That is, a particle is partly in state 1, and partly in state 2. We might call this state (0.5, 0.5), since if we measure the particle, there is a 50% chance of finding state 1, and a 50% chance of finding state 2. But this is the incorrect way of doing it!
The more correct way to characterizing the mixed state is with the square roots of the probabilities. Rather than writing (0.5, 0.5), we should write (0.707, 0.707), since 0.707 is about the square root of 0.5. But recall that every number has two square roots, one positive and one negative. Therefore, we can also have particle in the state (0.707, -0.707). If we measure this particle, we will still have a 50% chance of finding it in state 1, and a 50% chance of finding it in state 2.
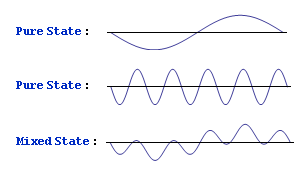
But there is a difference between (0.707, -0.707) and (0.707, +0.707)! A difference that can be experimentally tested! I can demonstrate it with a simple diagram:
One of the mixed states is mostly on the left side, while the other is mostly on the right. This is perhaps an oversimplified situation, but the point is that they are indeed different. When I said that superposition is just a matter of addition, I fibbed a bit. Superposition is a matter of addition and subtraction.When people hear about mixed states, the natural reaction is to say, "Doesn't it make more sense to say the particle is in one state or the other, and we just don't know which it is?" Yes, that would make more sense, wouldn't it? But that's not the reality. If we were merely ignorant of the particle's true state, we would be able to fully characterize it with probabilities (0.5, 0.5). But to fully characterize a particle in a mixed state, we need the square roots of the probabilities. That makes all the difference in the world. A difference that has been experimentally tested and confirmed.
Multiple energies, Multiple locations
What I called a pure state before, that was actually just a pure energy state. That was a state in which the particle has exactly one energy, where we have no probability of observing any other energy. But there are other kinds of pure states. For example, we might have a pure position state. It looks like this:
This is a wavefunction that is zero everywhere, except in the middle, where there is an infinitely high spike. The spike indicates that there is a 100% probability that the particle is in exactly that position. Such a pure position state is not actually possible in the real world; because of the uncertainty principle, the position is always guaranteed to be uncertain. But nonetheless, it is still instructive to consider this mathematical construction.As I said before, if you add two pure states together, you get a mixed state. If you add an infinite number of pure states together, you get a mixed state. Imagine adding lots of these infinte spikes together, side-by-side. Individually, they are really spiky, but added together, they can make a smooth curve like this one:
Any wavefunction can be constructed this way. Every wavefunction is in a mixed position state. Every particle is in multiple locations at once. It's not weird, it's absolutely commonplace. We just never see it because it's so darn small, the size of an atom. But it acts on every atom. Have I mentioned that it's what keeps atoms from collapsing?Similarly, we can consider other kinds of states. For example, if we have a cat in a box, it might be in a "dead" state, an "alive" state, or a superposition of the two. That's the idea behind the Schrodinger's cat thought experiment. Of course, a simultaneously dead and alive cat sounds completely ridiculous, and it is! I mean, under certain interpretations, it theoretically makes sense, but there's absolutely no way to test it. For all practical purposes, the wavefunction of the cat collapses instantaneously, and thus the cat can be said to be in a pure dead state or in a pure living state.
Questions!
I am just a humble physics undergrad, but I'm sure I could answer at least a few questions. I'm probably terribly unclear and incomplete in my explanations, but if no one asks, I never find out. [Warning! I am not an appropriate source for any sort formal research or learning. This much should be obvious.]
14 comments:
If I survive a quantum suicide experiment, is there a way to tell whether I'm just a partial fragment of my former self in a mixed state or whether I'm just really, really lucky?
No, there is no way to tell the difference. Theoretically, and only under the Many Worlds Interpretation, yes, but for all practical purposes, no. We can tell the difference for small, well-controlled sets of particles, but probably never for anything so large as a virus.
hello guys,i am little bit unaware of this probability principles,the doubt arised to me is why should one consider square root o the probability for mixed states
The principle of superposition states that we can add and subtract wavefunctions, rather than the probabilities themselves. The square of the wavefunction is interpreted as probability. Thus, the square-root of the probability gives you a wavefunction.
There's no particular reason why it should be so, but that's what we see in experiments. For example, we can observe two probability waves interfere destructively (meaning they cancel each other out because one is positive and the other is negative).
actually, quantum superposition isn't a strictly physical thing. it is actually a consequence of the linear algebra upon which QM is based. in maths-speak, it means that a vector can be written as an sum of vectors in a different basis, kind of like when you ask a chinese person to translate a particular character of their alphabet and the give you a bunch of english words, that when taken together mean the same as the original chinese word.
But isn't it strange to say that superposition is necessarily a consequence of the math and not the physical thing? I mean ideally, the math would perfectly describe the physical thing; or, in other words, the physical thing would be a perfect embodiment of the math. In that case the distinction is pretty meaningless.
On the other hand, if you're saying that the physical things aren't perfect embodiments of the math, then you're effectively saying QM is somehow wrong. Aren't you?
Nice. This is something I've been wondering about for a while. There wouldn't by luck be any chance of getting the previous writeup and this one in .pdf format, for archival and future reference?
No, I have no plans to convert anything to pdf.
hi guys, i am a bit confused. Geometrical interpretation of mixed state like (a1 + a2) or (a1-a2) is understandable. but how do I interpret a state like (a1+ i.a2) where i is a complex number.
Vin,
Whenever computing probabilities in quantum mechanics, you always calculate the square of the magnitude of the wavefunction (or equivalently, multiply the wavefunction by its own complex conjugate). So even if the wavefunction has an imaginary component, this still results in real, positive probabilities. Does this answer your question?
Your description is incorrect. Superpositions are not mixed states, they are pure states. A particle that is in "two states at once" (that is, for which a measurement on an observable could produce two results) is nevertheless in a pure state. Each vector in the Hilbert space representing that property in question is a pure state, even if it is a superposition. Mixed states are more akin to classical statistical ensembles of particles, not quantum superpositions.
Statist,
You are correct, and I have misused the term. What I refer to as "mixed states" are merely pure states that can be broken up into a superposition of different eigenstates.
As a layperson of physics, I don't understand why superposition says a particle is everywhere at once, since I don't see any particles. All I see are waves being combined with others.
And yes, I understand that a particle isn't there until a wave function collapses. But on the other hand, isn't superposition a more mathematical extrapolation than what may be happening? Especially if one were to think of an electron as a form of standing wave where the particle isn't manifested until it collapses?
It is important to talk about superposition if you want a predictive theory. Whenever you measure the position of an electron, it may appear to have a definite position, but to predict how it behaves between measurements, we need to speak of a wavefunction.
Post a Comment