Gödel's modal ontological argument

Update 2015: I wrote a new series on ontological arguments.

Previously, I've explained a simple ontological argument, and also a modal ontological argument. However, there's another modal ontological argument which interests me: That which was proposed by Kurt Gödel. It's Gödel's ontological argument!

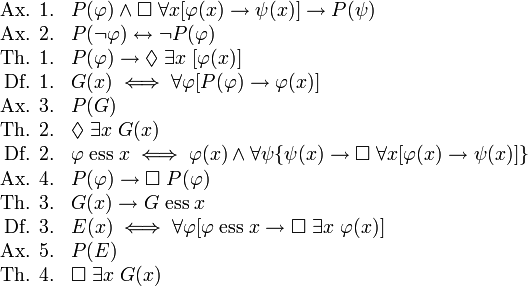It's all so clear now! There must exist an x such that G(x)! (That is, God exists!)

What's that, you weren't convinced? Indeed, most skeptics would be unimpressed, since it looks so obscurantist. The argument seems to work solely on the principle of "blinded by Science!", or in this case, "blinded by Symbolic Logic!" Obviously, the proof doesn't really prove what it purports to prove, or the argument would be backed by philosophers everywhere. I certainly don't expect everyone to have the knowledge to be able to read the proof, much less pinpoint the precise location where it might go wrong.

However, as it happens, I had already taught myself a bit of modal logic, so I thought, why not try reading the proof, you know, for fun? I'm not going to go through it step by step (unless my readers really want me to), but instead, I'll outline the basic idea, and explain where I think a flaw is. [Update: By request, I went through the proof, step by step.]

The basic idea of Gödel's argument is based on the previous modal ontological argument. According to the modal ontological argument, God, by definition, necessarily exists. Therefore, if it's even possible that God exists, then God must exist in all possible worlds, including the one which we happen to live in. The problem is that we still have yet to show that God is possible.

And this is where Gödel comes in. Gödel supplies a proof of the fact that God is possible.

But first, we must define a "property". A property is an attribute of an object. For example, we might let "x" denote a particular apple, and "R" denote the property of being red. Thus R(x) is the statement "This apple is red." Gödel's central insight was to categorize some properties as "positive" and other properties as "not positive". We use P(R) to denote the statement "The property of being red is a positive property."

Gödel never tells us exactly what he means by "positive". That's because it doesn't really matter what exactly it means. The proof works, regardless. All that matters is that the positive properties obey a few axioms.

• Axiom 1: If property A is positive, and if property A entails property B, then B is positive.
  
• Axiom 2: If property A is positive, then the property not-A is not positive.
  
• Axiom 3: The property G is a positive property. (G is the property of being "God-like"; an object with property G has all positive properties)
  
• Axiom 4: If a property is positive, then it is positive in all possible worlds.
  
• Axiom 5: Necessary existence is a positive property.

The question is, is it even possible to construct a concept of "positive" such that it obeys all these axioms? Maybe, maybe not. The power in these axioms is that they seem so intuitive. If they were not intuitive, then I would simply disagree with the axioms, and be done with it. But since they are intuitive, I must pinpoint exactly why our intuition goes wrong. And then I can disagree with the axioms, and be done with it.

Let's focus on axiom 1. What does it mean for property A to entail property B? That means that for every possible object in every possible world, if it has property A, then it also has property B. Of course, if there is not a single object in any of the possible worlds with property A, then A automatically entails B.

For example, let's consider the property of being an invisible pink unicorn, which we will call U. Let us presume that U is an impossible property. There is not a single object in any possible world which has the property U. Therefore, U entails O, which is the property of being omnipotent. I mean, have you met any invisible pink unicorns which are not omnipotent? I doubt it. Similarly, U entails every property. All of them, every single one. U entails the property of being solid dark blue, the property of being a flying spaghetti monster, and the property of not being a flying spaghetti monster.

So if U were a positive property, then every property would be positive. Obviously, this is not the case (see axiom 2). Therefore, U is not a positive property.

But this contradicts our intuition of what makes something positive (and recall that these axioms were based on intuition in the first place). Surely, there are some things which are positive, but sadly impossible. For instance, the invisible pink unicorn may be impossible, but if she existed, she would surely be a force for good. Wouldn't I be justified in saying that U is a positive property? No, because if I assume U is "positive", then I am essentially assuming that U is possible.

You might notice that in axiom 3, we assume G, the property of being God-like, is a positive property. Here, we're basically assuming that G is possible. Oops!

[An aside: In discussions of Gödel's modal ontological argument, people will inevitably start talking about Gödel himself. I haven't really seen any evidence that Gödel necessarily saw this argument as anything more than an interesting exercise in modal logic. Which is, of course, how I see it.]

The unlinking torus

A little known fact: If you have a torus (a donut-shaped tube) with a hole in it, then it is possible to turn it inside-out. I will leave the details for you to work out, but rest assured that it is possible.

That's the inspiration for this puzzle (which I basically stole from Martin Gardner).

Here we have a torus. There's a big hole in it so that we can turn it inside-out. There is also a ring (in red) painted on the outside of the torus. There is also a ring (in dark blue) painted on the inside of the torus. These two rings are linked.

But suppose I turned the tube inside-out. Then the red ring will be on the inside, while the blue ring will be on the outside. Then the rings will no longer be linked!

Did I really manage to unlink the rings? If so, how?

See the solution

Handshakes solution

See the original puzzle

Here's a grid showing the unique solution. "M" represents Martin, and "P" represents his partner. Person 1 is partnered with 2, 3 with 4, 5 with 6, and 7 with 8.

The proof of this solution follows.

There are ten people at the party. No one shakes hands with themself or with their partner. Therefore, each person can shake hands with up to eight different people. So when Martin asks everyone how many times they shook hands, each person gives an answer that is between 0 and 8. He got nine different answers, meaning that each number 0-8 was given exactly once.

The person who shook hands 8 times must have shaken hands with everyone at the party but his/her own partner. Therefore, the partner must be the single party-goer who shook hands 0 times.

Similarly, the person who answered 7 must be the partner of the person who answered 1. This is because the person who answered 7 must have shaken hands with everyone except his/her partner, and the person who answered 0. The person who answered 1 must have shaken hands with the person who answered 8, and no one else.

Similarly, the people who answered 6 and 2 must be partnered. The same goes for 5 and 3. The last couple must have both answered 4. One of those people must be Martin, since everyone except Martin gave a different answer to his question.

Therefore, Martin shook hands with four people.

This puzzle was solved by Baumann Eduard and Secret Squirrel together, with one proving possibility, the other proving uniqueness. Hooray for teamwork!

True Christians

True Christians. It's a phrase I'm sure you've all heard before. Do I even need to provide examples of how it is used?

"I agree, most people behave badly, but then, most of those people aren't true Christians."

"Hitler wasn't a true Christian (he was Catholic!)."

You get the idea.

This is a really silly piece of rhetoric to use on an atheist. What do I care which Christians are "true" and which are "fake"? I don't have any reason to think that "true Christians" are any better than just regular old Christians. Just because it has the word "true" in it doesn't really mean they are any more truthful. I could define the "perfect numbers" to be the set {6, 28, 496, ...}, but that doesn't actually mean that my life would be made more perfect if I worked six days a week instead of five.

Even if I do take the word "true" seriously, the phrase "true Christian" only seems to mean someone who is true to Christianity. I believe Christianity is a mistake, therefore, I believe true Christians are true to a mistake, more so than the fake Christians. Is this supposed to impress me?

And even if I did think Christianity were essentially good, this piece of rhetoric would still fail at its basic goal. The basic goal is to say, "I am different from those other people. I am on God's side." What is wrong with all those other people? They only claim to be Christian. They're not actually Christian, in essence.

But if you claim to be a "true Christian", you're still in the same boat as all those other people. You only claim to be Christian. How do I know that you are actually, truly Christian? You think I'll take your word for it? In fact, how do you know? How would you know you are truly Christian, if you think the vast majority of Christians do not know? In a misguided attempt at arrogance, you've ended up disparaging a group which, as far as anyone knows, includes yourself.

And if you define true Christians to be those Christians which do good works, then how do I know that the set of all true Christians has any relation to the set of people who claim to be true Christians? How do I know that it has any relation to any particular set of Christian doctrines? I rather doubt that it does, considering how many doctrines there are which have no relevance to anything outside of religion.

Plug: The Professor and the Dominatrix

A while ago, an author sent out his book, The Professor and the Dominatrix out to many secular student groups, including BASS, our own group. Its themes are atheism and sex, so he apparently thought we would approve of it. But it's even worse than bad fan fiction. The author babbles a lot, has a strange fixation with cocks. He not only caricatures the Christians, but also various ethnic groups and queers.

I didn't read it myself, of course. Deja, a member of BASS, read it for us and gave a presentation on it: The Professor and the Dominatrix. (Oh, for the record, I wasn't the one who added in the NSFW picture of the dolls.) It was better when Deja was speaking over it, but the powerpoint presentation is still definitely worth seeing by itself.

If that weren't enough, the author seems to be taking all the negative reviews of his book rather personally. You should see some of his correspondence with blagger Jen. This is the sort of thing that happens when you insert yourself into your novel as the Gary Stu hero.

Great spiraling black holes!

Around this time is when you start to hear about everyone else's exciting plans for the summer. Hey, wait, I have one of those too! I got a research job at Caltech working with LIGO, the Laser Interferometer Gravitational Wave Observatory. It's probably not as glamorous as it sounds, but boy does it sound awesome.

Let's begin with the observatories. There is one observatory in Louisiana, and two in Washington state. The gravitational wave detector consists of two lasers which go in perpendicular directions. Each laser is 4 km (2.5 miles) long, and encased in a vacuum pipe. Once the lasers have bounced back and forth in their tubes many times, they recombine and interfere with each other. By looking at the interference pattern of the lasers, we can determine the difference in length of the two laser paths. And by that, I mean we can measure the difference very sensitively, down to 10^-18 meters. This is about a thousand times smaller than an a proton.

One of the Washington detectors. Credit: NASA

Why do we want to measure so sensitively the length of a laser path? It all goes back to Einstein.

Albert Einstein is most famous for his theories of Special Relativity and General Relativity. Special Relativity describes how physics behaves when things move near the speed of light. General Relativity is the theory which incorporates both Special Relativity and gravity. In fact, General Relativity is the theory which replaces the classical theory of gravity. The classical laws are very accurate under most conditions, but are decidedly incorrect nearby very massive objects and when things are moving near the speed of light.

In a way, it's rather surprising that General Relativity and classical gravity could possibly be describing the same thing. Classical gravity describes everything in terms of forces. General Relativity describes gravity as a distortion of the space-time topology. In other words, gravity influences the distances and time-intervals between different events. These small distortions cause a straight line through time appear to be curved, as if it were acted upon by some force.

One of the predictions of General Relativity is the existence of gravitational waves. Gravitational waves are analogous to electromagnetic waves (aka light). Electromagnetic waves are fluctuations in the electric and magnetic fields. Gravitational waves are fluctuations in the space-time topology. Electromagnetic waves are created whenever an electrically charged object accelerates. Gravitational waves are created whenever a massive object accelerates. Both kinds of waves are characterized by a frequency, which tells you how quickly the waves fluctuate. If a gravitational wave passes through the LIGO detector, it will cause the two laser arms to fluctuate in length. If the gravitational wave has a frequency of 40 Hz, then the lengths will fluctuate 40 times per second.

LIGO is only sensitive enough to detect gravitational waves with frequency 40 Hz or higher. At lower frequencies, it becomes too difficult to distinguish between gravitational waves and regular old earthquake activity.

What could possibly cause a gravitational wave of more than 40 Hz? Gravitational waves are caused by accelerating massive objects. For example, the earth is constantly accelerating towards the sun because it is in a circular orbit. But this should only cause gravitational waves with frequencies of about 1 per year. However, we might be able to detect orbiting objects if they are orbiting much faster than the earth. One of the objects we are interested in is the binary black hole* system. Black holes are very massive objects, and also very small. So two black holes could be orbiting very quickly and closely to each other. If a pair of black holes is what it takes, then let's look for black holes!

*It could also be any other type of massive astrophysical compact halo object (MACHO), like a neutron star.

One other thing about gravitational waves, is that they carry energy, just like light does. As two black holes orbit each other, they emit energy in the form of gravitational waves. This causes the black holes to slowly lose energy, falling slowly towards each other. Because they're closer together, the "force" of gravity is stronger, and they orbit faster and faster. The picture we have here is of two black holes, spiraling around each other, getting closer together and moving faster. Eventually, they collide, coalescing into a single black hole. When there is only one black hole left, it no longer emits gravitational waves, and its signal disappears.

This could really use some animation. So I found some animations on the net from the Numerical Relativity Group.

The detection of gravitational waves is not only a way to test Einstein's theory of General Relativity under new conditions, it is also a new way to do astronomy. It's much like how we build telescopes to detect electromagnetic waves from far away sources. We can use gravitational waves to detect objects like binary black holes, as well as exploding stars, and a certain kind of pulsar. Scientists are also trying to detect something analogous to the cosmic microwave background radiation, only it would be cosmic gravitational background radiation. It would be very difficult to detect, but it comes from a very early point in the universe's history, far earlier than even the microwave background radiation.

I'm taking a break

I'm busy. I'll be back in a week or two.

When I come back, there's so much I want to write. I want to talk about my summer plans. I want to talk about induction and science. I want to talk about more "fun" arguments for a god, even if I'm the only one who thinks they're any fun. I also want to talk about LGBTA (lesbian gay bisexual transsexual asexual) stuff. Though I've supported queer rights all along, I've recently had renewed interest in the topic and I'll be sure to find stuff to write about.

Well Ordering Math Myth

Right now I'm taking a course in analysis, so we were covering the Peano Axioms. The Peano Axioms define the set of natural numbers. The fifth Peano Axiom is the famous axiom of induction, which states the following:

Let P be a set. If P contains zero as an element, and if "n is an element of P" implies "n+1 is an element of P" for all natural numbers n, then P contains the entire set of natural numbers.

A good analogy is dominoes:

Let there be an infinite line of dominoes. If you knock down the first domino, and if each domino knocks down the domino after it, then all dominoes will get knocked over.

Each domino in the infinite line of dominoes corresponds to a natural number. The very first domino corresponds to the number zero. The set P is just the set of dominoes which will be knocked over.

I've always wondered why it is we need the axiom of induction. It just seems so obvious and intuitive. Of course you're going to knock down all the dominoes. How could it be any other way? Why do we need to assume, as a fundamental axiom, that the dominoes will all fall over? Is there some system of dominoes which would not all get knocked over?

It turns out that the answer is yes. It's quite simple really. Let's say we have not one, but two infinite rows of dominoes. These dominoes obey all the other Peano Axioms, but they do not obey the axiom of induction. Because if you knock down that first domino, you're only going to get that first row of dominoes, and miss the second row completely.

Supposedly, the axiom of induction is equivalent to the so-called Well Ordering Principle (WOP). The WOP states that given any non-empty set of natural numbers, there is always a least natural number in the set. That is, given any set of dominoes, no matter how many you pick, you will always be able to pick out the single domino which comes first, before all the others.

So, funny story. In my analysis class, we were trying to use the first four Peano Axioms and the Well Ordering Principle to prove the axiom of induction. I pointed out a flaw in the professor's proof. I thought maybe there was some quick fix, some detail we missed. But the next day, the professor came in and explained why I was correct. You cannot prove the axiom of induction from the WOP.

In fact, it is possible to devise a set of numbers which obeys the WOP, but does not obey induction. Let me go back to the domino analogy. Let's say we have two infinite rows of dominoes as shown below.
If you take any set of dominoes, you can always pick out a single domino which occurs first. That is, there will always be one, and only one domino which is to the left of all the others in the set. And yet, if you knock the very first domino in the set, then you will only be able to knock down the first infinite row of dominoes, leaving the second one untouched.

The dominoes represent a simple set of numbers, which looks like {0,1/2, 1, 3/2, 2, 5/2, 3, 7/2, ...}. The first row of dominoes represents all the whole numbers {0, 1, 2, 3, ...}. The second row of dominoes represents all the non-whole numbers {1/2, 3/2, 5/2, 7/2, ...}. Induction will only get you all the whole numbers, the first row of dominoes. And yet, this system of numbers obeys all the other Peano axioms and the WOP.

This is really strange, because I've been told many times that the WOP is equivalent to induction. You can use induction to prove the WOP, and you can use the WOP to prove induction. But it's not true! It was all a myth, propagated even by the most authoritative sources. Usually, when they try to prove the axiom of induction from the WOP, they either implicitly or explicitly start with the natural numbers. But you don't have the natural numbers until you first have the axiom of induction! All you really end up showing is that given WOP and induction, you can prove induction.

The Kennewick Man

On my archaeology midterm, I answered a question incorrectly about the Kennewick Man. Later, I looked it up, and look what I found:

According to NAGPRA, if human remains are found on federal lands and their cultural affiliation to a Native American tribe can be established, the affiliated tribe can claim them. The Umatilla tribe of Native Americans requested custody of the remains, wanting to bury them according to tribal tradition. However, their claim was contested by researchers hoping to study the remains; if Kennewick Man has no direct connection to any modern-day native tribe, then NAGPRA should not apply.

The Umatilla argued that their creation myths say that their people have been present on their historical territory since the dawn of time, so a government holding that Kennewick Man is not Native American is tantamount to the government's rejection of their religious beliefs.

I found this hilarious, at least at first. The courts can't reject the Umatilla tribe's claim of connection to the Kennewick man, because that would be rejecting their religious beliefs? Hilarious.

So what happens if I believe, as part of my religion, that Native Americans, in ancient times, defected from and killed off a righteous civilization? What if I believed--religiously, of course--that Native Americans deserved retribution for this crime? You can't say that they did nothing to deserve it, because that would be tantamount to rejecting my religious beliefs!

If you thought I was just making that religion up, you'd be wrong. This has historically been believed by Mormons.

After reading that, I looked around Wikipedia some more (you know how it is), and I read about the American Indian Religious Freedom Act. I have somewhat mixed feelings about this. I'm all for religious freedom, but under most circumstances, religious people should not be allowed to do things that would otherwise be illegal. I consider the AIRF act to be a sort of grandfathering in of Native American religions. If a group started a new religion and just claimed that, say, marijuana was part of their religious practices, then I doubt that this would be legal, because this new religion has not been grandfathered in.

50% chance of doomsday

The Daily Show With Jon Stewart	M - Th 11p / 10c
Large Hadron Collider
thedailyshow.com
Daily Show Full Episodes Economic Crisis First 100 Days

I love how Walter Wagner claims that the LHC has a fifty percent chance of destroying the earth. See, there are two possibilities: the LHC will destroy the earth, or it won't. Each outcome has a one in two chance, so it's fifty-fifty.

The fatal flaw is that he's assuming all possibilities are equally likely. That assumption may work for coin flips, or for rolling dice, or for picking colored marbles out of a black bag, but it fails spectacularly when applied to less artificial situations, doesn't it?

Cosmic rays are constantly bombarding the earth, sun, and other observable bodies. In the entire history of the earth, about 3 x 10²² cosmic rays have hit the earth with higher energies than the energy of the LHC collisions (from the LSAG report). So it's sort of like we've already flipped the coin thirty thousand billion billion times, and gotten heads every time. I think it's safe to say at this point that it's a two-headed coin.