Two Identical Dissections

Everybody enjoying their holidays? I'm keeping the blog lighter than usual for the moment, so here's a short puzzler for you all. Have a happy new year!


Cut each polygon above into two congruent pieces. "Congruent" means exactly the same, but they may be rotated or reflected.

You may specify the coordinates of your cut (taking the lower left dot as origin).

ETA: I have posted the solutions here.

Our Christmas Traditions

After talking to the internet a bit, I've decided to talk a bit about what I do for the holidays. See, I've always held the conviction, since starting this blog, that my life is fundamentally uninteresting to anyone but myself. To talk about myself all the time would be solely self-serving, and thus be completely out of place on a blog. But after talking a bit with the internet, I've found that there is much interest in the question of "How do you celebrate the holidays?" Despite the strong aspect of tradition in the holidays, there is a surprising amount of variation in how people celebrate. Even though my own family's traditions seem absolutely normal to me, I suppose they are still worth sharing so that we all might compare our different visions of normal.

It shouldn’t be too surprising that I celebrate Christmas. Contrary to popular myth, leaving religion does not mean that you lose your Christmas or any holiday. That is, unless you don’t like celebrating holidays, then no one is forcing you. In any case, the rest of my family celebrates Christmas. For us, it is a very family-oriented holiday. Christmas involves two or three family gatherings (and then there’s another on New Year’s Eve).

Family gatherings are pretty fun. They always have dinners of the sort that leave excess food. And there’s also plenty of time to talk to extended family, watch movies, play board games with cousins, and everything. Sometimes I play some Christmas music on the flute, although privately I am not a fan (an entire month out of every year is dedicated to a relatively small set of music, so of course it annoys me!) It’s actually not particularly different from any of the other family gatherings we have for other holidays. Except, of course, for the presents.

There always seems to be an abundance of presents. Honestly, I don’t know how the rest of the family does it. I don’t think I could ever pick out a gift or two for each of my many cousins, aunts, and uncles, and yet my mother seems to do just that. She’s a very good selector of gifts too. As for me, I seem to have a phobia of shopping.

When I was younger, I used to get a few presents which were marked “From: Santa”. That was the extent to which my family pushed Santa. There were only a few presents from Santa, and they were not clearly any different from the other presents. I do not recall a time when I believed in Santa. I thought of Santa as something I was supposed to pretend I believed in. Because that’s what all the adults are clearly doing. But I’ve always been a bit incredulous that anyone could really believe in Santa. I’m almost inclined to think that true Santa belief only exists in the movies. I’m even more incredulous that any parents would go so far as to dress up in a Santa suit in order to fool their kids. Don’t they only do that in the movies? The whole “fool your kids about Santa” tradition seems rather alien and excessively theatrical to me.

Another “tradition” that I think only really exists in movies and Christmas TV specials, is the practice of all the kids waking up early Christmas morning, and running down the stairs to find lots of new presents under the Christmas tree. We do have a staircase, but there’s hardly any sense in running down excitedly, unless you want to be overly dramatic about it. Most of those presents have been sitting, wrapped, under the Christmas tree (always a real one, covered with a ridiculous assortment of ornaments) for the last week or so, and most of them we open at family gatherings, not at home. We do have stockings though, even if we have no chimney to hang them over.

So tell me readers, was this as boring as I thought it was (be honest), or was it fascinating because of how differently you celebrate the holidays?

Imaginary paradox

Following my proof of the obvious, I thought it might be fun to prove the impossible. Math paradoxes!

Well, of course you all know about the proof of 1=0? It's included below for completeness.

Let a = b
a*a = b*a
a*a - b*b = b*a - b*b
(a+b)(a-b) = b(a-b)
a+b = b
a = 0
Let a = 1
1 = 0

The experienced algebraist quickly spots the error. One of the steps in the proof is an illegal move.

The following proof also makes an illegal move somewhere, but it breaks a rule that most people haven't ever heard of.

We start with Euler's formula:

e^ix = cos(x) + i*sin(x)

Here, "i" is used to denote the square root of -1. Euler's formula is far from a mere mathematical curiosity. I do not exaggerate when I say we use it all the time in physics. Euler's formula is the main reason that imaginary numbers are of any use at all. But I digress.

Using Euler's formula, we know...

e^iπ = -1
(e^iπ)ⁱ = (-1)ⁱ
(-1)ⁱ = e^iπi = e^-π

But then...

e^i3π = -1
(e^i3π)ⁱ = (-1)ⁱ
(-1)ⁱ = e^i3πi = e^-3π

Therefore, e^-π = e^-3π. But clearly this is wrong. Therefore, our proof is wrong. But where?

"Doubt" trailer

This movie trailer intrigues me. I think maybe I want to see this movie now.



This not a comment specific to this movie, but I was just thinking about how much hype The Golden Compass got because it was, shocker of shockers, anti-religious. Or, supposedly it was. The first book had a rather anti-dogmatic sentiment, and the later books were much more explicit about it, but the movie itself was just too crappy to convey any of that. The point is that everyone got so worked up about a movie just because it supposedly touched on religion, and not in a positive way. Before you know it, Christians are boycotting it, and atheists want to watch it just to spite Bill Donahue.

Everyone was entirely lacking perspective. Lots of films and other fictional media touch upon religion. Has anyone here seen Chocolat? Fiddler on the Roof? Contact? Come on, I hardly watch any movies, so I'm sure a typical person can think of plenty more. Does a film really need to be explicit about it for people to take notice? What's so much better about a movie that clearly comes down against religion? Please. Have some taste.

Same goes for music. No need to get all excited about some guy just because he *cough* raps against religion.

Axial Tilt: The Milankovitch Cycles

 [Note: This is not an original image, but the website I was crediting now appears defunct]

Last year, I explained how, exactly, axial tilt causes seasons. This year, I will explain how axial tilt changes over time in what we call the Milankovitch Cycles. The Earth's orbit and spin do not stay constant forever, but change over thousands of years. These changes are much too slow to cause seasons, but they can cause much larger climate changes like ice ages. There are three Milankovitch Cycles:

Precession

I've previously discussed the precession of the Earth, but here is the shorter rehash. Although the Earth's axial tilt is always about 23.5 degrees offset from the orbital plane, the direction of the tilt moves around in a circle every 25,700 years. The cause of this change is the gravity of the sun and moon acting upon Earth's equatorial bulge. Got it?

To understand how this affects climate, we're going to have to understand different kinds of years. Isn't there only one kind of year, you ask? No, there are actually many, many different kinds of years with slightly different definitions and lengths. What do we mean by "year" anyway? If we mean the time it takes for the Earth to complete a full orbit, then what we want is the sidereal year. However, that is not the kind of year that our calendar is based on! Our calendar is based on the time it takes for Earth to complete four seasons, the tropical year. Every tropical year, there is exactly one summer solstice, when the Earth's rotation axis is tilted towards the sun. But because precession changes the direction of Earth's tilt, the summer solstice actually occurs at a slightly different location of Earth's orbit every year. The tropical year is shorter than the sidereal year by about 20 minutes.

But when we're talking about long term climate changes, we're also interested in a third type of year. The Earth's orbit is not a perfect circle, and there exists a point in the Earth's orbit when it is closest to the sun. This closest point is called the perihelion, and it occurs around January 3rd. The gravity from other planets causes the perihelion to occur at a slightly different point in Earth's orbit every year. The time it takes to get from perihelion to perihelion is called the anomalistic year. The anomalistic year is longer than the sidereal year by about 5 minutes.

The reason precession affects climate has to do with the relative location of the summer solstice and perihelion. Currently, the summer solstice in the northern hemisphere is six months away from the perihelion. This makes for milder summers, since Earth is actually a little further away from the sun during the summer. Likewise, it makes for milder winters, since the Earth is closest to the sun during the summer. Incidentally, it also makes for longer summers, because the Earth orbits more slowly when it is further from the sun. However, because the anomalistic year is longer than the tropical year, there is a 21,000 year cycle, in which the perihelion moves from winter to summer and then back again. Therefore, seasons will grow stronger, and then milder again every 21,000 years.

Milder seasons favor ice ages because the summer isn't strong enough to completely melt the ice left over from the previous winter. If the ice never melts, it reflects more light from the sun, cooling Earth and starting a feedback loop which ultimately leads to an ice age. Of course, we could just as easily argue that a milder winter is less likely to start the ice cycle. Ultimately, it comes down to a more quantitative analysis along with experimental observation, and the current evidence says says that when the precession cycle favors milder seasons, it favors ice ages.

Of course, in the southern hemisphere, winter is in June, and summer is in December. When the northern hemisphere has milder seasons, the southern hemisphere has stronger seasons, and vice versa. Why would the 21,000 year cycle affect global climate if there's always one hemisphere with stronger seasons? I don't know the details, but basically, the northern hemisphere is more important (sorry South Africa!) because that's where the majority of the land mass is. Therefore, our current place in the precession cycle favors an ice age, but obviously its effect is being outweighed by something else, possibly the other Milankovitch cycles.

Obliquity

Earth's axial tilt is currently 23.5 degrees, but in fact this number changes slightly over time. Roughly every 41,000 years, the tilt cycles between 22.1 degrees and 24.5 degrees. The cause of this so called obliquity variation is, again, the sun, moon, and planets all tugging on Earth's equatorial bulge. Because axial tilt is the reason for the season, greater axial tilt will cause stronger seasons, and smaller axial tilt will cause milder seasons. Right now, we're near the middle of the cycle, and axial tilt is decreasing. Current arguments say that smaller tilt favors ice ages.

Interestingly, it has been shown that if the moon didn't exist, the Earth's axial tilt would change chaotically from 0 to 60 degrees, causing climate changes that would possibly be fatal to life. This is often used to argue that we're pretty damn lucky to have a moon. On the other hand, current theories say that a mars-sized object crashed into early Earth, and the resulting ejecta coalesced into the moon. If that collision had never occurred, the Earth would be spinning much faster now, and its axial tilt would be stable as a result.

Eccentricity

As I mentioned before, the Earth is not exactly circular. Its orbit is actually in the shape of an ellipse, with the sun placed at one focus of the ellipse. The "focus" is basically a mathematical point in an ellipse, slightly offset from the center. The ratio between the focus's distance from the center and the perihelion's distance from the center is called the eccentricity. An eccentricity near zero means a more circular orbit, and an eccentricity near one means a more elliptical orbit. Earth's eccentricity is about 0.017, meaning it is nearly a perfect circle.

For the same reasons that the perihelion changes its location in Earth's orbit over time, so eccentricity too changes over time. Because of complicated interactions with other planets, the eccentricity varies from 0 to 0.06 in not one but two cycles which last 100,000 years and 400,000 years. Our current eccentricity is a little below a maximum of the 100,000 year cycle, and will get lower over the next 30,000 years. A complicated math calculation shows that the maximum eccentricity causes up to 0.2% more sunlight than the minimum eccentricity, but that's a rather small effect. Perhaps more importantly, a higher eccentricity will amplify the effects of the precession cycle.

We would expect eccentricity to have the smallest effect of the Milankovitch cycles, but it's an unexplained observation that it in fact has the largest effect.

As an aside, we have a rather interesting way of measuring Earth's temperature over long periods of time. See, when marine plankton die, they leave their skeletons on the ocean floor. When the ocean is colder, their skeletons tend to preferentially incorporate the 18-oxygen isotope, which is basically a less common, but heavier version of the oxygen atom. Furthermore, in colder climates, 16-oxygen gets preferentially removed from the ocean and incorporated into the polar ice caps. Thus, during colder climates, the ocean floor sedimentary deposits tend to have a higher percentage of 18-oxygen isotopes. By digging into ocean sediments, we can use this to determine the Earth's temperature for the past several million years.

What the ocean sediments show is that before one million years ago, the biggest cycle in global climate had a period of about 41,000 years, suggesting that obliquity had the biggest effect. However, about a million years ago, something fundamentally changed about the Earth's climate system, and its biggest climate cycle now has a period of 100,000 years, with ice ages slightly lagging the times of low eccentricity. What changed? Why does only the 100,000 year cycle have an effect, while the effect of the 400,000 year cycle remains small? Obviously, there is still science to be done. The current best explanation seems to be that there are "complicated" interactions and feedback mechanisms which amplify the 100,000 year cycle, but obviously the devil is in the details.

So... Seasons: pretty important? Let's celebrate!

[This being a very information-heavy post, I should probably cite my main source: The Earth System, 2nd Ed. by Kump, Kasting, and Crane. Anyways, no one should be looking to my blog as a serious research resource.]

Guess the Meaning II

What phrase is suggested by this photo?

Man, I just realized how much cell phone cameras suck compared to real cameras.

No one smart and beautiful

As I was browsing the TV Tropes wiki, I suddenly got an idea. Maybe there's a perfectly good reason why nerds are stereotypically portrayed as ugly, socially inept, or crazy eccentric.

It could be because nerds in fact do display these qualities, and the stereotypes merely exaggerate them. But we don't like that answer, 'cause that would have negative implications about ourselves. Cognitive dissonance!

But anyways, in my sudden moment of what might be called "inspiration" by excessively optimistic folks on a good day, I had a different idea. There are few perfectly smart, well-adjusted, attractive individuals in fiction because that would fall into the Mary Sue archetype. The Mary Sue is a character that has everything going for her in unrealistic quantities. Everything in the story centers around Mary Sue, and the conflicts only exist so that she can overcome them. Though the Mary Sue is obviously the author's favorite, she often comes to be disliked by the audience. Why? Because she is unrealistic, we can't relate to her, and she has only one dimension: perfection.

The Mary Sue is frequently the result of the author placing him or herself into the story. That's why authors have trouble understanding why everyone else dislikes the character. "How can you not like her? She's perfect (like me)!" It's a little egotistical, but hey, we're all a little egotistical. Except me. I'm a paragon of humility.

But back to the original idea. Why is no one smart and beautiful in fiction? More generally, why is every smart person in fiction either: a) lacking common sense b) totally awkward c) ugly and weak or d) crazy eccentric? Have they never met a genius (like me)? If they had, they'd know that smart people are completely normal, except better in every respect. If I ever had the chance to write fiction, I would portray nerds realistically: we're practically oracles with both our earthly and unearthly wisdom, we dominate every party we set foot into, and there is no problem in the world that can't be solved by a bunch of people like us. Everyone will love us, and want to be us, as we achieve ultimate cultural power!

What about that one circle?

An example of bad reasoning:

"Science has explained most instances of X. Many turned out to be hoaxes. Others had completely natural explanations. But what about the unexplained instances of X? You can't explain them all away!"

If we were playing "Name That Fallacy", I would call this "remembering the hits, and forgetting the misses". But the interesting thing is that the argument acknowledges that there have been plenty of misses, as if acknowledging them would make them go away.

The first concrete example I can think of are crop circles.

Image taken from CircleMakers

Crop circles are a phenomenon that became popular in the 1980s. At first, they were simple circles, but in more recent times, much more complicated patterns have appeared like the one above. It's practically an art form nowadays. I think they look cool, don't you?

According to the mythology, crop circles are created by UFOs, which are always saucer shaped, of course. The UFOs land on a crop and make a circle. There were other theories too, such as whirlwinds or other weather. Now, I would have looked at this and immediately thought that they were man-made. Of course hindsight's 20/20 and I'm too young to understand the 1980s mindset. In any case, there's little point worrying about back then, because the current evidence is very clear. In 1991, two men confessed to making some of the earliest crop circles in England. Well, perhaps "confession" is the wrong word--more like letting the rest of us in on the joke. One of them is interviewed here (god I love this interview).

If that weren't enough, there's even a website "CircleMakers" for people who make these crop circles. Oh look, there's even a field guide. You could be making "unfakeable" crop circles in no time!

Anyways, while I'm sure this evidence convinces most people, there still exist UFOlogists who claim that at least some, if not all crop circles are made by UFOs. You see, even though some of the circles are explained by pranksters, this small group of people couldn't possibly have made every single pattern in the entire world. And even if there were enough circle makers, there exist some circles which are supposedly too complicated to be made by dedicated pranksters.

You can easily see the problem with this reasoning. We already have a sufficient explanation. Adding a second one is just unnecessary, and unlikely to be true. For every circle maker that has confessed, there are going to be other circle makers who chose not to. Just because not every circle has a known creator does not mean that our explanation is insufficient.

Going back to my main point, this is because our investigative ability is limited. We cannot thoroughly investigate every single instance of a phenomenon. Sometimes there are things that just make full investigation too difficult to be feasible. Sometimes there is simply no budget for it. Sometimes all evidence has already disappeared, lost to entropy, leaving the phenomenon permanently unexplained. Sometimes an investigation will even show a false positive, for a variety of reasons. For example, some people heard strange sounds at night which they thought were related to crop circles. Further investigation determined that it was a kind of bird, but what might we have thought if no one had ever figured it out?

But this is not to say that scientific investigation is useless. If done correctly, by the scientific method, tests will correctly discern truth most of the time, if it manages to discern anything at all. But if you ignore most of the results just to look at the few unexplained cases, you've just done away with any validity your analysis might have had. Sometimes, those few unexplained cases are indicative of a new paradigm, but more often than not, they're related to our limited methodology. We need a more compelling argument than the existence of a few unsolved cases.

Selected Putnam Problems

At least one reader (Susan!) expressed interest in seeing the Putnam problems.

For those not in the know, the William Lowell Putnam Competition is a national math competition intended for college undergrads such as myself. The yearly contest consists of twelve problems (rigorous proof required) and six hours' time. The problems range from moderate to very difficult. Well that's kind of subjective. A more enlightening description: a few thousand students participate each year, and the median (not the mean!) is roughly zero.

I have it on good authority that it's safe to talk about them now. You can refer to the Art of Problem Solving forums for a more complete discussion of the entire 2008 contest.

So here are three of the problems. I picked out easy ones with more of an "aha!" feel to them.

A1: Let f: ℝ² → ℝ be a function such that f(x,y) + f(y,z) + f(z,x) = 0 for all real numbers x, y, and z. Prove that there exists a function g: ℝ→ ℝ such that f(x,y) = g(x) - g(y) for all real numbers x and y.

A2: Alan and Barbara play a game in which they take turns filling entries of an initially empty 2008x2008 array. Alan plays first. At each turn, a player chooses a real number and places it in a vacant entry. The game ends when all the entries are filled. Alan wins if the determinant of the resulting matrix is nonzero; Barbara wins if it is zero. Which player has a winning strategy?

B1: What is the maximum number of rational points that can lie on a circle in ℝ² whose center is not a rational point? (A rational point is a point both of whose coordinates are rational numbers.)

How did I do, you ask? I think I got four correct, but I hear the graders are particularly harsh, so you never know. I didn't get A2 and B1, but they sure seemed obvious afterwards. If you're still curious, ask me in the comments.

2+2=4: a proof

In case you had any doubts, here is a proof that 2+2=4.

Of course, if by "2" we mean "apple" and by "4" we mean "orange", then the statement is false. It should be clear that "2+2=4" has a specific meaning, and if we change any of its meaning, we've changed the statement. Natural numbers, such as 2 or 4, have specific meanings. They are things which obey the Peano axioms. If they don't obey the Peano axioms, they are not really natural numbers, and we might as well be talking about apples and oranges.

The Peano axioms thoroughly logical and simple to state. But I'm not going to cover it in detail, since you can just peruse the Wikipedia article for more.

For every natural number n, the Peano axioms define the "successor of n", or S(n). Every natural number, except zero, is the successor of another natural number. All natural numbers can be expressed this way:

0
S(0)
S(S(0))
S(S(S(0)))
S(S(S(S(0))))
...

We have names for each of these numbers: 0, 1, 2, 3, 4, ...

And so, by "2+2=4", we really mean this:

S(S(0)) + S(S(0)) = S(S(S(S(0))))

Not only do natural numbers have a specific meaning, but the symbol "+" has a specific meaning. It is defined with the following two axioms:

n + 0 = n
n + S(m) = S(n + m)

So here's the rest of the proof:

S(S(0)) + S(S(0)) = S( S(S(0)) + S(0) )
= S( S( S(S(0)) + 0 ) )
= S(S(S(S(0))))

Fairly simple, eh? But, hey, maybe if you find a way to tap into the power of the other 90% of your brain, you will prove the impossible. Either that or your dreams will be crushed and the resulting cynicism will negatively affect the rest of your life.

A harder problem would be to prove that n + m = m + n. I think you might even have to use the axiom of induction for that one.

In other news, I'm taking the Putnam tomorrow! Also, I'm sure this will come as shocking news: I'm going to minor in math! Yay!

Fractal Results

These are the results of the requests I got for Newton's fractals. Each function generates a fractal that, in principle, covers the entire plane, but I only show a small window of it. When I talk about the "range" of the fractal, I am referring to the location and dimensions of the window I chose.

Susan asked for the hyperbolic trig functions. Actually, they look more or less the same as the regular trig functions, but that's okay because the trig functions turn out well.

This is the function cosh(z) in the range -.5 to .5 on the real (horizontal) axis, and -.5 to .5 on the imaginary (vertical) axis. Note that only the first six roots get unique colors--the rest are all black.


And this is the function tanh(z) in the range -3 to 3 in the real axis and -2 to 2 in the imaginary axis.

An anonymous commenter asked for the function e^-(ixcosx)+e^(xsinx). This is a complicated one, graphed from 0 to 2 in the real and imaginary axes. I suspect those black comb-shaped things are actually artifacts of my program, but it took such a long time to generate the fractal that I wasn't going to try to figure out how to get rid of them. Besides, they look cool.

Why I'm not a humanist

There is a certain virtue in avoiding "positive" labels. On the one hand, you want to present yourself positively. On the other hand, you don’t want to present yourself as better than everyone else.

I don't consider myself to be a humanist. What exactly does that tell you about me? Does it mean that I don't view the good of humanity to be the highest good? Does it mean that I don't believe in any sort of human dignity? Does it mean that I don't value rational human inquiry? No, silly. It just means that I don't like the word "humanist". Maybe I technically qualify as a humanist, but I never call myself one.

In the atheosphere, I nearly always see the word "humanism" in only one context. Humanism is meant to be the positive counterpart to atheism. Atheism tells you what we don't believe in, and humanism tells you what we do believe in. Atheism is just one aspect of a person, while humanism is a complete philosophy. For a word that's supposed to be all-encompassing, I find it odd that I only ever see it in one place.

I just don't ever see the necessity to use the word "humanist". For one thing, no one ever asks me, "What do you believe in, if not God?" except in my dreams (dreams I attribute to my large ego). And if someone did ask, I'd probably just say, "Life? Goodness?" (I might also add "induction" on account of being a fanatical inductionist.) If I responded, "Humanism," who would know what that means? Most importantly, I don't know what it means. I only know the many things that have been told to me. My sources are a little vague about the details, but whatever humanism is, I know it's good! A bit of liberal politics here, a bit of the-good-of-the-human-race there, a dose of church-state separation, a rejection of the supernatural, along with a compatibility with religion. I figure that if it's good, it must be somewhere in the mix (and guess where that leaves the non-humanist).

I have no patience for any of that. If I wanted to say in detail what I believe in, I'll deliver it in plain words that everyone understands, not in a mystery package that not even I understand. For all those humanists out there, maybe you understand what humanism is, but does everyone else understand it the same way you do?

Of course, to be fair, I myself go with the "skeptic" label, which is also a "positive" philosophy. And though I understand what I mean by skepticism, not everyone immediately understands it the same way I do. Call me a hypocrite if you will. But I understand these things, that people can have aversions to labels even if they agree with the ideas represented by the labels. Just because a person doesn't go by a label doesn't mean they go against everything the label stands for. This applies to all labels.

River-crossing solutions

See the original puzzle

1. The fox, chicken, and lettuce. Someone pointed out to me that it's usually stated as fox, chicken and corn. Well, sure, if you like your puzzles to make sense. :-)

Bring across the Chicken.
Come back with nothing.
Bring the fox across.
Take back the chicken.
Bring the lettuce across.
Bring the chicken across one last time.

2. Three missionaries and three cannibals. This one was solved by Secret Squïrrel. For those who didn't know, I give free linkage to the first solver of any puzzles. I appreciate it when other people write up the solution so I don't have to.

mmm ccc || nobody
mmm c || cc (2c ->)
mmm cc || c (<- 1c) mmm || ccc (2c ->)
mmm c || cc (<- 1c) m c || mm cc (2m ->)
mm cc || m c (<- 1m1c) cc || mmm c (2m ->)
ccc || mmm (<- 1c) Now the c come across in 3 trips.

I leave it as an exercise to the reader to find out how many missionaries and cannibals you can safely bring across if you have a boat that holds three people.

Why "pseudoskeptic" is a worthless label

A few weeks ago, the local skeptical group decided it would be a good idea to have "pseudoskepticism" as a topic. The idea is that we get to discuss what sort of mistakes denialists make, and in turn elucidate the definition of a "skeptic". It turned out that it wasn't a good topic after all. People really seemed to dislike the word "pseudoskeptic", though it's hard to properly convey what's so wrong about it.

More recently, Matt Nisbet, Scienceblog's notoriously uncharismatic proponent of "framing", attacked the word "denialism" on account of it being inflammatory. I don't know about that. It seems to me that if "denialism" is negative, it's not because of the word itself, but because of the content of its meaning (if that makes any sense). The content of its meaning isn't going to go away, no matter what we call it. But forget Nisbet. (Forget, I say!) My main point relates not to Nisbet but to this Respectfully Insolent response. As an afterthought, Orac says this in his response:

Of course, if you're less pugnacious than Mike, Mark, or me, in my benevolence, I'll suggest an alternative term other than "denier" or "denialist." Lately, I've started to like the term "pseudoskeptic." It captures the essence of what denialists do almost as much as the term "denialist." Remember, a true skeptic is always open to changing his or her mind if the evidence and science demand it.

No! Don't use "pseudoskeptic". It's bad!

The first thing that strikes me about the word "pseudoskeptic" is that it gets us into the "fake vs true" mode. It's the perfect setup for the No True Scottsman Fallacy. Every time I hear the word "pseudoskeptic", it practically begs to be replaced with the phrase, "not a True Skeptic (TM)". After all, if you've never heard the word, that's exactly what the conjunction of "pseudo" and "skeptic" will mean to you. If it came into popular use, I can just imagine the devolution of discussions. "You're a pseudoskeptic!" "No you're a pseudoskeptic!" I hate the word, I hate it!

If my worries seem farfetched, we only need look at the history of the word. (Skeptical history!) It's common knowledge (read: on Wikipedia) that the word was coined/popularized by one of the founders of CSICOP, Marcello Truzzi. CSICOP, the Committee for the Scientific Investigation of Claims of the Paranormal (now simply called CSI), was founded in 1976 as one of the first skeptical organizations to ever exist. Marcello Truzzi was the editor to CSICOP's official journal, The Zetetic. Unfortunately, Truzzi had some sort of falling out with CSICOP because he wanted to include pro-paranormal stuff in the journal. Truzzi left CSICOP, and founded his own journal, The Zetetic Scholar, which included arguments both for and against the paranormal. It was around this time that Truzzi said that the so-called skeptics were becoming pseudoskeptics.

The temptation to simply say, "No, you're a pseudoskeptic" is strong. In my mind, Truzzi was completely wrong, and CSICOP completely right. Truzzi's position was that of pyrrhonic skepticism, the position that we cannot know anything for sure. Pyrrhonic skepticism is wrong because we can know things, not with complete certainty, but with sufficient certainty. I can't know absolutely for sure that psychics don't exist, but I can be sufficiently sure, given the vast amounts of evidence, that they are vastly unlikely. There is a lot of merit to drawing tentative conclusions even when you're not completely sure. Truzzi's position is that of "fair and balanced" journalism, which simply portrays both sides of every issue equally, regardless of the relative merits of either side.

Truzzi, perhaps sensing that the word "pseudoskeptic" would simply bounce back at himself, decided to take another label for himself: "zetetic". A wise move, I say.

But doesn't "pseudoskeptic" have its uses? It seems like it would be useful against factions that call themselves skeptical, the epitome being the "Global Warming skeptics". Now, personally, I don't really think of them as fake skeptics. No, they are true skeptics, albeit under a different definition of skeptical. Skepticism means many different things, after all. When I use it, I refer to the method of determining the veracity of claims through rational and scientific thought. Other times, skepticism means something like Truzzi's zeteticism. In the case of Global Warming skeptics, it simply refers to a position of doubt. It's a moot point whether that doubt has been achieved through proper use of rational and scientific thought.

We don't have a monopoly on the meaning of "skepticism". But of course, we'd like to. Therefore, it's to our advantage if we disassociate the skeptical method from the position of Global Warming skepticism. To do that, we need to give them a different name. But "pseudoskepticism"? Please don't. In my benevolence, I'll suggest an alternative term other than "pseudoskeptic". Use "denier" or "denialist". The meaning of the term is obvious, even to someone who has never heard it before: "One who denies". It may have a slightly inflammatory connotation due to its connection to Holocaust denial, but that's pretty weak. Global Warming denial is distinct from Holocaust denial--I should have thought that obvious.

What the bleep do we know!? reviewed

Some of you may remember hearing about the film What the Bleep Do We Know!?, which came out in 2004. It’s a documentary that explains a rather new-agey interpretation of Quantum Mechanics, and how this might apply to consciousness and daily life. I know that this is old news, but when it comes to something as nearly mainstream as What the Bleep, it doesn’t hurt to revisit it one more time.

The Science

As the title of the movie suggests, one of the central messages of the movie is about how little we know. This is perhaps an honorable sentiment, discouraging arrogance and encouraging open-mindedness. It is in fact true that Quantum Mechanics has several different interpretations which are “up for grabs”. However, it’s not completely up for grabs; you do need to know a bit about the science in order to make an informed judgment on the interpretations. What the Bleep, betraying its supposed open-mindedness, gives you a very spotty and distorted view of the science.

Much of the Quantum Mechanics explanation occurs on "Duke Reginald's court of unending possibilities”, a basketball court governed by quantum mechanics. The film uses fancy effects to drive home the strangeness of quantum mechanics. When you aren’t looking, that basketball is in many places at once. When you look at the basketball, the possibilities collapse into one. What the film fails to mention, is that this is only really true on small scales. Every particle is in many places simultaneously, but most of those places are in a tiny region smaller than a nanometer.

That single omission, by itself, would be forgivable. I've seen worse. However, they go on to deliver a very wild interpretation of quantum mechanics: we choose the results of our observations. Really? So if we wanted, and believed, with every fiber of our being, we could choose to observe a basketball one meter to the left? Wouldn't that contradict quantum mechanics, which states that there is only a small probability of it appearing one meter to the left? I must have missed the "human will" term in Schrodinger's equation, because last I checked, the probabilities are completely independent of the observer's state of mind.

Furthermore, they've completely jumbled their interpretations of Quantum Mechanics. Presumably, they're going by the Copenhagen Interpretation because that's the only one with "observers" in it. Under the Copenhagen interpretation, when we observe objects, they "collapse" into a single possibility. However, "observer" is a technical term that has been abused here. The "observer" need not be human. The observer could simply be a measurement device. The device could be measuring millions of particles, but it will still collapse all of them, regardless of whether anyone is paying attention to the specific results. This is an undeniable experimental fact that must be explained by all viable interpretations of Quantum Mechanics.

You could say that the measurement device itself splits into many different possibilities. In one possibility, the device sees the particle here, and in the other possibility, the device sees the particle there. And then, when we look at the device, it collapses into only one of those possibilities. But then, if you like, you could also say that humans split into many different possibilities, and that no collapse is occurring at all. This is called the Many-Worlds Interpretation.

I'm glossing over all the details here, but this is still way better than what appeared in the film, which didn't even bother to name a single quantum interpretation.

The Copenhagen Interpretation and Many-Worlds Interpretation are the two most popular interpretations of quantum mechanics. In neither of them is the human mind so completely special that it's the only thing in the universe that can collapse quantum possibilities. Why should we think that consciousness plays any role if a mere measuring device gives the same experimental results?

Their flawed interpretation goes completely awry when interviewee Candace Pert goes on to say that human cells can collapse quantum possibilities, and therefore they are the smallest units of consciousness. This led into some rather boring scenes with anthropomorphic cells. So, let me get this straight. Because only human observers can cause quantum collapse (false!), consciousness must play a role. And then, because other things also cause quantum collapse, we reason that those other things must be conscious too. Garbage in, garbage out.

The Pseudoscience

You might think, so far, that the movie simply gets a bunch of details wrong about quantum mechanics. Yes, I'm a pretty harsh judge when it comes to quantum mechanics. However, they're not just wrong on obscure science details, they're wrong on common sense. These are some strange claims that were scattered throughout the movie:

1. Interviewee Joe Dispenza says that when people see a picture and when they imagine a picture, the same areas of the brain light up on scans. He goes on to claim that this means the brain doesn't know the difference between what it sees and what it remembers. I would have thought a guy like Dispenza would realize that a brain scan doesn't tell you absolutely everything about the state of your brain. Just because two brain scans look the same doesn't mean our brains can't tell the difference.
   
   
2. Interviewee Candace Pert claims that Native Americans initially could not see Columbus' ships approaching, because they had no concept of what a ship is. I'd say this is a good example (if it's true) of how we are likely to see the things we want to see, and miss things that we don't want to see. But the film reenacts the scene in the most literal way imaginable. The shaman cannot see the boat, but he can see the ripples. Only after much watching does the boat appear. I've got to wonder, even if the story were true, how would we know it was true?
   
   
3. Interviewee John Hagelin says that in a 1993 experiment, he got 4000 people to meditate in order to reduce crimes in Washington D.C. He claims the experiment successfully reduced crime rates by 25%. But 25% reduction compared to what? It was 25% reduction, as compared to the predictions of a model of their own construction. Great.
   
   
4. The film uses as a prominent example the water experiments of Masaru Emoto. Emoto attached words to glasses of water, and allowed them to form crystals. He then used microscopic photography to capture the resulting crystals. Of course, when the experimenters know exactly which word is attached to which glass, they'll easily be able to pick out whatever crystal best matches. It's perhaps an interesting photography project, but it totally fails as science.
   
   
5. Interviewee Micael Ledwith claims that if you accept with every "rudiment of your being", you can walk on water. What if I say with every rudiment of my being that you can't? Does that cancel it out or something?
   
   
6. Joe Dispenza says some pretty weird things about he "creates his day" through quantum mechanics. He claims lots of things happen that are unexplainable any other way. No examples, though. If you ask me, this is a much better example of people seeing only what they want to see than that Columbus thing.
   
   
7. The punchline: One of the interviewees is Ramtha, a 35,000 year old spirit-warrior from Atlantis. Ramtha is being channelled by a woman named JZ Knight. She says the funniest things through out the movie, but only in the credits does it say who she really is (I, of course, knew ahead of time). If you do some digging, you find that the entire movie was put out by the Ramtha School of Enlightenment. Of course, I'm just an amateur critic, not an investigative reporter, so you'll want to refer to Salon for the digging.
   

The Fable

One common response is, "What's so bad about it if it helps people?" After all, fables are false stories, but they still convey a moral message.

But if we say it's acceptable to use bad arguments when they come to the right conclusions, what's to stop people from using bad arguments to come to the wrong conclusions? What's to stop people from convincing themselves, for instance, that they really are listening to a 35,000 Atlantean spirit? In any case, if the "moral" of the film is so great, then it stands to reason that you should be able to find a good argument in favor of it. One that doesn't involve distortions of quantum mechanics or pseudoscience about transcendental meditation.

But I must say, it actually struck me how negative the message of the film was.

The most striking example came out of Emoto's water crystals. After showing the photos, a mysterious bystander says to the protagonist, "If thoughts will do that to water, imagine what our thoughts can do to us." That would have been a sorta maybe positive thing to say, if it weren't for the one water crystal photo that said "You make me sick. I will kill you." Apparently, if you think negative thoughts, you'll become ugly? The film also says that if you can't control your emotions, you must be addicted to them. Later in the film, this is shown to happen to the protagonist. I understand negative thoughts being bad and all, but should we really instill into people a fear of negativity? Fear of thought is very negative indeed.

On the more philosophical end, I find their use of quantum mechanics shockingly cynical. They make it very clear that without quantum mechanics, there is no free will. Several of the interviewees seem to think free will is vital to being able to truly live. I study physics, and I think it's really important and everything, but if it turns out that quantum mechanics is wrong, or if it turns out that it doesn't have a significant impact on free will, I think I'd still find the will to live. (I've got a fuller discussion of how quantum mechanics relates to free will here.)

In another example of questionable morals, interviewee Jeffrey Satinover states that some psychological problems are not really psychological problems, but the result of bad choices. That might seem like a positive thing to say to people who are trying to overcome their psychological problems, but you're also saying it to the people who have tried and failed. I guess now it's their own fault for failing. Later, the protagonist chucks her anxiety medication while a voiceover says "Try it out yourself". That may work for a few people, but just imagine the pain it would cause to everyone else.

Of course, not every "moral" in the movie was bad, and I am being a little nitpicky. But this is the sort of thing that happens when you accept bad arguments just because they give you good morals. You'll end up getting not-so-good morals too. All at the price of distorting science. Was it worth it?

Extra links:

Skeptico: Excellent review, with a much more complete list of links

Salon: exposes the Ramtha cult behind the film

Blogging Heads: physicist David Albert talks about how the film misrepresented him through editting

On generalizations

"Generalizations are always evil"

"Generally speaking, anyways"

Are generalizations intrinsically good or evil? Neither, obviously.

As an amateur critic, I talk all the time about people and their beliefs. I could either use an anecdote, implicitly generalizing my experiences to a larger whole, or I could skip that step and talk about groups of people as if they were abstract entities. Or I could stop being a critic altogether. Obviously, I have no business unconditionally condemning generalizations. They're all I have.

However, generalizations can obviously be abused. On the extreme end is racism and other bigotry. One could argue that the evil is in the falsity of such generalizations. Women and ethnic minorities are not actually inferior to white males. Homosexuals are not actually perversions created by the Devil. But perhaps a bit of the problem is in the generalization itself? How might we correct for this?

I think a little intuitive statistics goes a long way. Simply put, generalizations apply to groups, and not to individuals.

Let's say you've scientifically proven that a certain group of people usually exhibits a certain trait X. If you take any subset of the group, and count how many people have trait X, you're going to have a certain amount of theoretical uncertainty, just due to random sampling. That uncertainty is roughly sqrt(N) people, where N is the size of the sample. So if you have only a single individual, the uncertainty is roughly one person.

I'm sure somewhere in there is the message, "You can choose", just like they told us in Minority Report.

And that only goes for scientifically proven generalizations. I can assure you that any generalizations I make are not scientific at all. If I were to estimate, I'd say 0% of the statistics and generalizations on this website are backed up by scientific evidence. They should be treated with the appropriate skepticism.

This is why I take personality tests with a grain of salt. Even if they are indeed scientifically tested (which is more than we can say of many personality tests), they're still based on the idea that I should take statistical results and apply them to myself. The uncertainty is one person!

On the flip side, if generalizations can't be applied to individuals, this leaves a rationale for people hold onto their preconceived prejudices despite the clear existence of counterexamples. Hrrrm...

Random Links

I'm awfully busy this week, and there's so much good stuff out there right now. So enjoy!

Catholics for Choice - They published a long document criticizing the Catholic League. The Catholic League deserves every bit of it.

SkepticBlog - Skeptic - That Name Thing again - An enlightening view on the meaning of skepticism

The Thinker - Critical thinking and Skepticism. They're overlapping, but distinct.

Uncertain Principles - There is no moral content in Many Worlds Theory or Multiverse Cosmology (which are two completely different things btw). I'm 100% behind Chad here.

Cuddly Atheism - Precocious - I love the "thank you" letter from the Catholic School.

River-crossing classics

For this week's puzzle, we will have two simple classics. Remember: in the world of puzzles, simple is not necessarily bad, and challenging is not necessarily good.

1. A man must cross the river with a fox, a chicken, and some cabbage. There is only one boat, and only the man can row it, and he can only take one companion at a time. For obvious reasons, he cannot leave the fox alone with the chicken or leave the chicken alone with the cabbage. How can he do it?

2. Three missionaries and three cannibals must cross a river (geez, whoever wrote this one had a dark sense of humor). They have a single boat that can only carry two people, and there must be at least one person rowing it. If at any time, there are more cannibals than missionaries on either side of the river, the cannibals will eat the missionaries. How can everyone get across alive?

Update: Solution has been posted

Adventures in atheist advertising

In recent news, the American Humanist Association (AHA) paid for a bus ad campaign in Washington D.C. This is what the ad says:

If you're interested in the response to the ad, Friendly Atheist has lots of links and an interview with an AHA representative.

I think it's rather interesting to watch how the atheists react to the ad. I see the same pattern of reactions occurring all the time. Some of us enthusiastically support the cause, while the rest of us are left wondering if it was really that good of an idea. You can count me in the latter group, at least with respect to the bus campaign, but allow me to feign some objectivity here.

Oh, the usual questions bounce back and forth. Are we targeting atheists, theists, or the middle? Is it intended to be an attack on religion, a call to freethinkers, or just a call for discussion? If religious people think it's an attack, is that acceptable or not? If not, is it our fault or their fault? Who are we trying to convince, if anyone, and of what? Are we imitating religion, and is that bad? How many people are we "reaching" and how many people are we pushing away? And to sum up all previous questions, was the ad campaign good, or bad?

Sometimes, I despair of answering such questions. I'll stick to physics, thank you.

Perhaps, if I try to explain it, I will help myself understand?

The plain message itself is not too hard to understand. "Why believe in a god? Just be good for goodness' sake." It is basically asserting the secular humanist* position: acting morally is worth it for its own sake, and that believing in a god or religion is not required. It's actually a rather mild message, I think. No, seriously, everyone should agree that goodness is its own reward. I would have agreed when I was Catholic (but apparently that's only because I wasn't Bill Donahue). For those who don't agree, obviously the message wasn't intended for them. The ad only states a position; there certainly wasn't enough space to argue the point. It is not intended to convince anyone, but rather to promote awareness. If you're a nontheist, you aren't alone, and if you're a theist, there are happy people with different beliefs.

*I find it really odd that the American Humanist Association advocates exclusively secular humanism. What about religious humanists? Aren't they important too?

You may also have noticed that the ad uses a slogan nearly like one of the lines in "Santa Claus is Coming to Town". This is simply intended to be a cutesy nod to the season. It's worth noting that many nontheists celebrate Christmas and enjoy the season, at least as much as everyone else does. Some don't celebrate, and there's nothing wrong with that. The so-called "War on Christmas" is a complete fabrication*, and as far as I can tell, there is absolutely no motivation to start such a war. Thus, the Christmasy tone of the ad is not meant to be mocking or subversive. It's simply because Christmas songs are a common cultural touching point, even among nontheists.

*Okay, I guess there's the "happy holidays" vs "merry Christmas" thing, but that's just tremendously silly.

But intentions aside, some people will react badly. The primary problem is that the question "Why believe in a god?" comes off as a challenge. If you ask atheist supporters about this, half of them say religious people are simply reading too much into it, while the other half say, yes it's a challenge, and what's wrong with that? What's wrong is that no one's going to be convinced by a one-liner on a bus, duh. And it builds on the impression that atheists have nothing to do with their time but challenge religion.

And yes, maybe religious people are reading too much into it. It's not really meant to be a challenge. It's just hard to navigate all the little pitfalls and convey a message without offending a bunch of people. But we have to navigate it. If you try to make a subtle point about how hard it is to avoid offending people, it's not going to come accross in a bus ad. So deal.

Another reason people react negatively is because it's similar to those religious billboards. You know, like those godspeaks boards that say things like, "We need to talk. -God" I don't propose to know what their motivation is, but the website says it's to, "create a spiritual climate and get people to think about a daily relationship with a loving and relevant God." Oh, so they can feel good about themselves as they think about all the people who've been inspired by a one-liner on a billboard. They're totally tacky, and I'm glad they don't appear where I live. Doesn't the AHA ad serve the same purpose, to make people feel better about themselves? No, I'd argue that the ultimate purpose is to increase visibility of secular humanism. But it's still totally tacky, at least according to my gut reaction.

Of course there will be negative reactions, but how could we possibly do any better? I dunno. I sort of like this billboard campaign better. It says, "Don't believe in God? You are not alone." It's straight to the point: we nontheists exist. It doesn't challenge religion, it doesn't need to. If we so wanted to challenge religion, advertisement isn't the proper route. Of course, even when the billboard clearly doesn't try to challenge religion, it still considered "controversial". So why bother trying to be "nice" if it'll be controversial either way? I'm not sure sometimes... Because... it's a matter of degree, and we only need generate as much controversy as is worthwhile.

Pill Puzzle solution

See the original puzzle

This was solved by Yoo of Stochastic Scribbles:

...cut each of the indistinguishable pills in half, being very careful not to mix them up, cut the last remaining pill A into half, too, and take a half from each pill each day.

If that wasn't clear enough, you basically add an extra pill A to your pile, and then eat half of each pill. Save the left over half-pills for tomorrow.

This is one of my favorite puzzles. It's simple and elegant, and requires a bit of lateral, but logical thought. I don't know about anyone else, but when I see a puzzle I like, I try to think up a small variation that would produce another cool puzzle. I can't think of one for the Pill Puzzle yet, but maybe one day.

Request a Fractal!

In a previous post, I explained how to make fractals using Newton's method. These fractals can be generated by a java program I wrote for a high school project. The main input is a mathematical function.

So you give me a mathematical function, and I will make a fractal out of it!

You do not need to understand how Newton's Method works to make a request.

The rules:

• Be creative! A simple function (like f(x) = x²) might not produce anything interesting. More complicated functions may not produce anything interesting either, but I can adjust them to make them interesting.
  
• You may use any of the following in your function:
• Any arithmetic: addition, subtraction, multiplication, division, in absolutely any combination.
  
• Imaginary numbers (represented by "i")
• Trigonometric functions: sin, cos, tan, etc.
• Inverse trigonometric functions: arcsin, arccos, arctan, etc.
• Exponentials: e^x, x^(-1/2), x^x, x^i, and so on.
• Logarithms
• Any, absolutely any combination of the above. Even something like x*(cos(tan(x))^(i/x))-log(i+arctan(x)) is possible. But please don't suggest anything that crazy.

More complicated functions tend to generate more complicated fractals; simpler functions tend to generate simpler (more elegant?) fractals. For examples refer to the bottom of my previous post.

Oh, and here's one more example to throw out there. This Mandelbrot look-alike was generated with the function (x+1)*sqrt(x).

I will post a bunch of these at a later date.

Fractals from Newton's Method

Today, I will explain how I created this:

This is a fractal. A fractal is a pattern that contains smaller versions of itself. But it's not just any fractal. It's a fractal I created from something called Newton's method.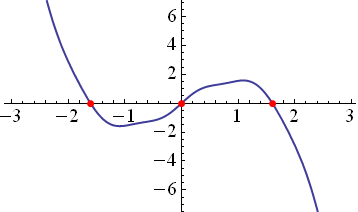

Newton's Method

Let's say we have a mathematical function called f(x). I chose one specifically for this demonstration. Here is a graph:

A very common math problem is to find the "roots" of f(x). That means you're trying to find what numbers "x" can you use to make f(x) equal to zero. In a graph, that means that it touches the horizontal axis. In the picture above, the roots are all shown with red dots. You can see that one root is zero, and the others are near 2 and -2.

It's easy for me to make an instant estimate of the roots, but that's because I had a computer graph it for me. What if I were, say, Isaac Newton, and I had no computers? What if I wanted a really accurate estimate of the roots? I would invent a new mathematical method and name it after myself, of course. And that's what Newton did.

Newton's method relies on the fact that most functions are more or less straight. The graph of f(x) sure doesn't look straight--it curves all over the place. But if we zoomed on just one part of the graph, it would be almost straight. An almost-straight line is almost like a straight line. So it stands to reason that an almost-straight line has almost the same root as a straight line.

In the above graph, I started by "guessing" the location of the root at -2. Using this guess, I drew a "tangent line" to f(x). This tangent line is a straight line that just barely touches f(x) at the blue point. Finding a tangent line is a standard method from calculus. If we just find the root of the tangent line, we know it must be fairly close to the root of f(x).

Notice that we started with an initial guess of -2, and we got a much better guess. That means we can take any guess and make it into a better guess! There's no reason to stop there. All we need to do is repeat the process, starting with a better guess each time. You can get a very good estimate of the root of f(x) very quickly.

When you guess badly...

The trouble with Newton's method is that functions aren't really straight. They can curve all over the place! Let's see what happens when I try a different initial guess of -1.

After only one iterations, it looks like we're getting a very accurate approximation of the root near 2. But wait, didn't we initially guess -1? Even though our initial guess is between the first two roots, we end up finding the third root. Newton would probably consider this a bad guess, because we didn't find the root we wanted to. However, we have a different idea in mind.

We want to answer the question: Given any initial guess, which root will we eventually find?

Though the original method was invented in the time of Newton, this is a question that they never could have answered. What if a single guess bounces around for a while, before finding a root? You really need to use a computer to test all the possibilities. So that's what I did.


(Click for a bigger picture.) When you guess badly, you get a fractal!

Allow me to explain the meaning of the fractal. Each color corresponds to a different root. The darkness of the color corresponds to the number of iterations required to get the root. Of course, you never quite reach the root exactly. But once it's within a certain distance, the computer decides that it's close enough. Some guesses are so bad that they don't ever find any root (at least as far as my computer has tried). Those guesses are indicated in white.

It's actually not too surprising that this method would result in fractals. First you have the large regions which correspond to good guesses. Then you have small regions of bad guesses. These "bad guess" regions map to the rest of the number line. And so, the "bad guess" regions will end up looking like smaller versions of the entire fractal.

More complex, More fractal

So far, I've only explained how to make a 1-dimensional fractal. The one-dimensional fractal maps the number line to different colors. But at the top, I showed you a 2-dimensional fractal. The 2-dimensional fractal maps the complex plane to different colors.

The complex plane is a sort of extension of the number line into two dimensions. It includes the "real" numbers, like -1, pi, and sqrt(2). It also includes "imaginary" numbers, like "i", the square root of negative one. And then there are complex numbers, which are in the form a+b*i. The number "a" is called the real part, and "b" is called the imaginary part. The real part is represented by the horizontal position on the complex plane, while the imaginary part is represented by the vertical position.

Otherwise, the method is exactly the same. Only now, it's prettier. And there might be new roots that were previously hidden.

The fractal at the top was generated using the function f(x) = x^3-1

But I have tried much more complicated functions as well. Some of you might recognize this one, because I use it as my avatar in certain internet locales.

This one was generated by the function f(x) = x*cos(x)^i. This function has only one root. The black regions correspond to guesses that never lead to the root.

This was generated by the function f(x) = log(x) + x. I also made a nice desktop-sized version, 'cause it's so awesome.

This is the function f(x) = e^x - x. This function has an infinite number of roots, only two of which are being shown.

This is f(x) = log(x²). I had posted this on my blog last Christmas. The blue "ornaments" are actually an exploit in my computer program; they wouldn't normally be there.

These are all generated using a Java program that I made for a high school project. I have found it very fun to experiment with this math-to-art device. I want you all to have a taste of that. So... later, I will be taking requests for mathematical functions!

Away with All Gods! debate

This is just a pointer to my latest contribution to the BASS website. I attended a debate called "Away With All Gods! Possibility or Fantasy?"

Because I believe in the power of a good teaser quote...

Bartchy played the “Stalin” card. Normally, I would groan at this cliche, but I think it is a fair point against Communism. Sunsara’s response?

Read the entire thing here.

And while I'm at it, I might as well toss some other links around too.

Skepticblog: Tao of Traditional Medicine - Skepticblog is exceeding expectations so far

Greta Christina: Proud -- and Bitterly Disappointed - post-election commentary, way better than the prop 8 post I had too-quickly assembled.

Belief, acceptance, etc.

Something that ever slightly irritates me: skeptical word aversions! I'm not allowed to "know" anything because that would imply that I'm dogmatic. I'm not allowed to "believe" anything, because science isn't about belief. I'm not allowed to "prove" anything because science can never prove anything. Seriously, relax!

I think all of us here realize that scientific proof is not absolute. I think we all realize that very little is truly certain. Does that mean that we have to constrain our language?

I find I have a habit of inserting lots of qualifiers into my language, such as "I think", "it seems that", or "nearly". I try to cut down on the qualifiers, because I want to have more language variety. It should go without saying that everything I ever write is only something that I think. Explicitly saying "I think" serves only to emphasize. It's there to emphasize uncertainty, or show unwillingness to speak for other people, or simply for style. I might have similar reasons for wanting to use a word like "know" or "believe". I don't see why these word-options should be off-limits.

There is a certain breed of essay that draws fine distinctions between words. Many draw a distinction between belief and acceptance. See, belief means dogmatically accepting things despite evidence to the contrary. Acceptance means tentatively believing things because they're currently backed up by evidence. The fundamental flaw with this type of analysis is that I have no reason to agree with the definitions. Maybe when some people say they believe, they mean taking as an article of faith, but that's not what I mean. When I say I believe in science, I mean that I believe in all the established scientific theories because they have been established by sound practice of the scientific method.

Colloquially, the difference between synonyms like "accept" and "believe" is just a matter of connotation and context. "Belief" is indeed used a lot in the context of religion. That doesn't mean religion is its only appropriate context. It does, however, mean that it carries a tiny bit of religious connotation wherever it goes. So I understand wanting to avoid the word most of the time. I understand wanting to draw a distinction between religious and scientific knowledge at every mention. But there's no reason to be anal about word distinctions when they don't even concretely exist. If you can explain the difference between "acceptance" and "belief", then you can also explain the difference between "scientific belief" and "religious belief".

Unhappy about prop 8

It's the day after election day. Are we allowed to talk about stuff that isn't election yet? No? Well, okay...

I'll drop the act--obviously I'm writing of my own free will, and therefore must enjoy doing so.

Obama wins in landslide. I assure you that I am excited about this, even if I'm not much interested in conveying my excitement.

What I do wish to convey is my displeasure about prop 8, the gay marriage ban. It passed. Why, California, oh why must you be so regressive?

As I understand it, there are basically three arguments against gay marriage. There's the religious conservative argument, the secular conservative argument, and the libertarian argument.

The religious conservative argument gets the most contempt, and is most deserved of contempt. Religious arguments can only justify that which you already believed. So it's not a justification at all, but rather, a sign of underlying prejudice. This "justification" deserves no place in politics.

The libertarian argument is that marriage should not be recognized by the government at all. That would be great, or maybe not, but either way it's beside the point. Right now, marriage is recognized by the government, so we might as well be fair about it. Once we get privatization of marriage on the ballot, maybe then we'll talk about it.

The secular conservative argument goes that marriage serves a specific purpose (ie raising children), and gay marriage lacks something vital to that purpose. Put a different way, marriage is a privilege, not a right. I'm fairly sure that gay couples can adopt and raise children at least as well as single parents can. Moreover, if a straight couple chooses not to have children (or is incapable due to fertility issues), we wouldn't want to ban their marriage. The difficulty of implementing a ban on infertile marriages is beside the point--we wouldn't ban it no matter how easy it would be to do so. And the "privilege" vs "right" thing is also beside the point. Either way, it's unfair to grant this privilege/right to some people and not to others. It's racist by word substitution.

I think the secular arguments against gay marriage are BS. Nobody would find these compelling unless they had an interest in finding them compelling. Basically, I think the supporters of prop 8 are a bunch of authoritarians. Authoritarians only believe these subpar arguments because they're on the side of the "proper" authorities, because they're supported by the Republican party. I wouldn't normally do this kind of armchair psychology, but I'm doing it now 'cause I'm so unhappy about the prop 8 results.

On a lighter note...

I really liked yesterday's Dinosaur Comic.



Oh, I think we're all a little racist by word substitution.

The Pill Puzzle

You are on an unbelievably strict medical prescription. Every morning you have to take exactly one pill A and one pill B. You must keep this up for a month, or there will be dire consequences to your health. You have just enough pills to last you the month, and you can't afford to go to the pharmacist to get more.

And so, you are dismayed when halfway through the month, you make a mistake. Right after putting one of pill A in your hand, you accidentally poured two of pill B in your hand. The pharmacists apparently didn't have the foresight to make pills A and B different colors or anything. Now you have three indistinguishable pills in your hand, and you're not sure what to do with them.

How can you keep up with your prescriptions without having to go to the pharmacist to get more pills?

see the solution

Politics!

How about them politics?

I just realized that I almost forgot to participate in that great blogging tradition of aggressively volunteering my thoughts about politics onto my readers near election. You know, because obviously that's what my readers came for--my ever-frequent comments about politics.

Uh, yeah, so I'm voting for Obama. It seems like a fairly obvious choice. Surely you see how compelling a case I make. That is what makes me a great political commentator.

Also important is voting No on Prop 8. Go LGBT rights! Seriously, I hear it will be close.

You should all vote exactly the way I do. That way, it's effectively like I have more voting power.

More importantly, simply vote! It's a well known fact in statistics that the uncertainty of a random sample is 100/sqrt(N) %, where N is the size of the sample (ie the number of voters). That means that one more random voter increases accuracy by 50/(N^1.5) %. Amazing! Of course, it's not really random, which means my analysis is completely BS, but don't tell that to your emotional brain.

Skepticism vs Atheism

As the regular readers know, I'm a member of the campus group called BASS, which stands for Bruin Alliance of Skeptics and Secularists. Note that the A does not stand for atheism. It isn't an atheist club, but it is. We advocate skepticism and secularism, which are not atheist-exclusive (I would hope not), but we're also the only group on campus to represent atheists.

Does that mean our group has two roles, or one? I don't think anyone would go so far as to say we should exclude theists, but there are a number of people who think of skepticism and atheism as the same thing, or closely related things. This is debatable. However, I think they are two different ideas, and I think you should think so too.

I will begin by conceding that skepticism and atheism are related. At the very least, they are correlated. But I think it's more than that. Skepticism actually causes people to become atheists, and atheism causes people to become skeptics. Anecdotally, I became an atheist because I carefully considered arguments while under a skeptical mindset (meaning, an open-minded, but critical mindset). And many atheists are highly sympathetic to the goals of skepticism, because they realize that religion isn't the only source of strange beliefs out there.

Furthermore, I think there are good reasons underlying the causational link. Not that skepticism logically entails atheism, or anything so direct. But I do think atheism is more in the spirit of skepticism than theism is. I think the idea of appealing to an unknowable entity in order to explain the universe, or for pretty much any purpose at all, is not good skeptical practice. Even for deism or fideism, my thoughts are along the lines of, "I don't find that very compelling, and I don't think you should find it compelling either."

But of course I would think these things. Of course I think atheism is more correct than its alternatives. I wouldn't be an atheist if I didn't.

The thing is, there are a ton of things that cause disagreement among skeptics. When I first subscribed to Skeptic magazine, I found that I disagreed with a third to a half of it. That is totally how it should be. Obviously, if there's an article about investigating a paranormal claim, I would expect it to be a well-designed investigation with a more or less definitive conclusion. But a lot of these are opinion articles, or they are detailed interpretations of complicated bodies of evidence. If you're not picking out lots of specific details that you disagree with, you're not doing it right.

Religion is very clearly within the region of "stuff that skeptics disagree about all the time". And it's a very popular topic too, because everyone seems to have a unique opinion about it. I've spent years in the atheist and skeptical blogospheres, and I still occasionally see a perspective that is unusual and surprising, and not in a bad way either. I find that the variance of religious perspectives is much greater than the mere difference between atheism and theism. If we were to exclude theists from the skeptical movement, to be consistent, we'd have to exclude a lot of atheists too. We couldn't possibly be so conformist.

To finish this off, I'd like to make two imperfect comparisons to give two different angles on how religion relates to skepticism.

First, religion is like politics. It is not a standard skeptical topic, but skeptics certainly tend to be politically conscious, and tend to enjoy discussing it. Libertarianism is not considered to be the same as skepticism, partly because less than half of skeptics are libertarians, but also because it's a completely different idea. Even if every skeptic were a libertarian, and if skepticism really did lead directly to libertarianism, we would still not consider the same thing. It's a difference of area of application, and a difference of method and conclusion. If you agree with the skeptical method, but by a strange twist of reasoning, come to an uncommon conclusion on one particular non-standard topic, you're still a skeptic.

Second, theists are like women or ethnic minorities. Lamentably, there aren't many of them in the skeptical movement. For whatever reasons, skeptics tend to be predominantly white males. There should be more minorities and women! Not because we want to be able to say, "We're so diverse and tolerant," but because we should be equal opportunity. I don't like the idea that half of the population is for whatever reason less likely to be skeptical than the other half. Similarly, I don't like the idea that religious people are less likely to be skeptical than the nonreligious. I don't care if there's a good reason for it. It's still sad.